wykres
Adam: Wykres liczby zespolonej
Mam narysowac zbior liczby zespolonej spelniajacy warunek
|z−2+3i|<4
więc
|x−2+i(y+3)|<4
√(x−2)2+(y+3)2
x−2+y+3<4
ale jak to narysować?
20 lis 01:04
Qulka:
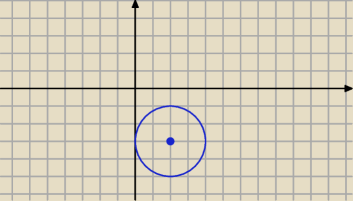
i wszystko co w środku kółecczka
20 lis 01:20
Janek191:
To jest wnętrze koła o środku ( 2 ; − 3) i r = 4
20 lis 01:21
Janek191:
Bo
√( x −2)2 + (y + 3)2 < 4 ; po podniesieniu do kwadratu mamy
(x − 2)2 + ( y + 3)2 < 42
a to jest wnętrze koła o S = ( 2, − 3) i r = 4
20 lis 01:36
Adam: Aaaa, faktycznie! Nie zauwazylem tego, dziekuje bardzo!

20 lis 02:02
Adam: Czy dobrze mysle, ze wykres dla |z−1|=|1+5i−z| to bedzie parabola, ale wykres jest tylko w
| | 25−5√3 | | 25+5√3 | |
punktach |
| oraz |
| na osi x? |
| | 2 | | 2 | |
20 lis 17:17
Mila:
ad. 17:17
Symetralna odcinka
20 lis 17:21
Adam: A dlaczego tak?
20 lis 17:22
zombi: Moduł liczby zespolonej, można interpretować jak na płaszczyźnie euklidesowej (Oxy) jako
odległość dwóch punktów.
Przykładowo
|z+i| = |x+yi+i| = |x+(y+1)i| =
√x2+(y+1)2. A przecież to nic innego jak odległość punktu
(x,y) od punktu (0,−1).
Bo przecież jeśli masz policzyć odległość dwóch punktów (x
1,y
1) i (x
2,y
2) w R
2 (Oxy)
to liczysz jako
d =
√(x1−x2)2 + (y1−y2)2 = |z
1−z
2|, gdzie z
1 = x
1+y
1i oraz z
2 = x
2+y
2i.
Taki więc jeśli mamy |z+z
1| = |z+z
2| oznacza to, że punkt z = x+yi = (x,y) jest równo
oddalony od
punktu z
1 oraz punktu z
2. A definicja symetralnej wyraźnie mówi, że jest to prosta, której
punkty są równo odległe od obu punktów odcinka o końca w z
1 i z
2.
Nie bój się liczb zespolonych, tu jest tyle analogii pomiędzy R
2, że każda osoba, która wie co
nie co o płaszczyźnie euklidesowej powinna się czuć swobodnie z liczbami zespolonymi.

20 lis 17:33
Mila:
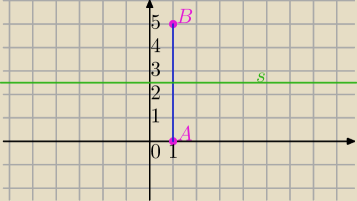
|z−1|=|1+5i−z| ⇔
|z−1|=|z−(1+5i)|
to będzie symetralna odcinka o końcach (1,0) i (1,5)
Wykażę to obliczeniami:
z=x+iy
|x+iy−1|=|1+5i−x−iy|
|(x−1)+iy|=|(1−x)+i*(5−y)|
√(x−1)2+y2=
√(1−x)2+(5−y)2⇔
y
2=25−10y+y
2
10y=25
y=2,5
==============
Zapamiętaj
|z−z
0|=|z−z
1| symetralna odcinka o końcach w z
0,z
1
|z−z
0|=a, a>0 okrąg o środku w z
0 i r=a
20 lis 18:17
Adam: Dziękuję wam bardzo

Dzięki wskazówce użytkownika zombi doszedłem do takiego samego
rozwiązania jak Ty mi podałaś

Właśnie nie mogę sobie wbić do głowy tego co mi napisałaś
jako zapamiętaj, niby to wiem, a ciągle coś kombinuję

20 lis 23:40
 i wszystko co w środku kółecczka
i wszystko co w środku kółecczka


 |z−1|=|1+5i−z| ⇔
|z−1|=|z−(1+5i)|
to będzie symetralna odcinka o końcach (1,0) i (1,5)
Wykażę to obliczeniami:
z=x+iy
|x+iy−1|=|1+5i−x−iy|
|(x−1)+iy|=|(1−x)+i*(5−y)|
√(x−1)2+y2=√(1−x)2+(5−y)2⇔
y2=25−10y+y2
10y=25
y=2,5
==============
Zapamiętaj
|z−z0|=|z−z1| symetralna odcinka o końcach w z0,z1
|z−z0|=a, a>0 okrąg o środku w z0 i r=a
|z−1|=|1+5i−z| ⇔
|z−1|=|z−(1+5i)|
to będzie symetralna odcinka o końcach (1,0) i (1,5)
Wykażę to obliczeniami:
z=x+iy
|x+iy−1|=|1+5i−x−iy|
|(x−1)+iy|=|(1−x)+i*(5−y)|
√(x−1)2+y2=√(1−x)2+(5−y)2⇔
y2=25−10y+y2
10y=25
y=2,5
==============
Zapamiętaj
|z−z0|=|z−z1| symetralna odcinka o końcach w z0,z1
|z−z0|=a, a>0 okrąg o środku w z0 i r=a
 Dzięki wskazówce użytkownika zombi doszedłem do takiego samego
rozwiązania jak Ty mi podałaś
Dzięki wskazówce użytkownika zombi doszedłem do takiego samego
rozwiązania jak Ty mi podałaś  Właśnie nie mogę sobie wbić do głowy tego co mi napisałaś
jako zapamiętaj, niby to wiem, a ciągle coś kombinuję
Właśnie nie mogę sobie wbić do głowy tego co mi napisałaś
jako zapamiętaj, niby to wiem, a ciągle coś kombinuję