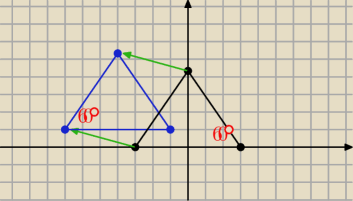
Oblicz pole części wspólnej trójkąta ABC i jego obrazu w przesunięciu o wektor v Zocha: Oblicz pole części wspólnej trójkąta ABC i jego obrazu w przesunięciu o wektor v=[−4,1]. A(−3,0) B(3,0) C(0,3√2)

Zocha: BŁAD tam ma być 3√3 w punkcie C

Qulka: bok małego 2−√3/3 więc pole

	(2−√3/3)2√3
P=		=13√3/12 −1
	4

Janek191: y = 1 y = a x + b A = ( −3, 0) B = ( 0, 4) więc 0 = −3 a + b 4 = b czyli 0 = − 3 a + 4 ⇒ 3a = 4 ⇒ a ={4}{3}

	4
y =		x + 4
	3

Rozwiązuję układ y = 1

	4
y =		x + 4
	3

−−−−−−−−−−

	4
1 =		x + 4
	3

	4
− 3 =		x
	3

	9
x = −
	4

======== Długośc boku małego Δ równobocznego

	9		9		5
a = − 1 − ( −		) = − 1 +		=
	4		4		4

Janek191: To wyżej jest źle Tam jest C = ( 0, 3√3 )

Qulka: jak weźmiesz prostą AC o wzorze y=√3x+3√3 i zrobisz metodą Janka to wyjdzie mój wynik