Prosze o pomoc w rozwiązaniu ;) krystynka : Na okręgu o promieniu √3 opisano trapez równoramienny ABCD o dłuższej podstawie AB i krótszej CD. Punkt styczności S dzieli ramię BC tak, że (|CS|)/(|SB|) = 1/3 Oblicz: a) długość ramienia tego trapezu b) cosinus kąta ABD

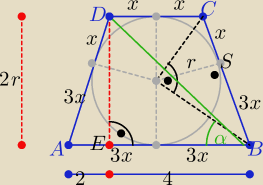
Eta: x>0 r²=x*3x ⇒ 3=3x² ⇒ x²=1 ⇒x=1 to |BC|=|AD|=4x=4 |AB|=6x=6 to |EB|=4x=4 i |ED|=h=2r=2√3 z tw. Pitagorasa w ΔEBD |DB|=√12+16= 2√7

	|EB|
cosα=		= .........
	|DB|

krystynka : A dlaczgo r jest obliczone w ten sposób?

krystynka : Dobrze nie ważne juz, dziękuję bardzo za pomoc juz wszystko rozumiem

pyzia: a dlaczego r jest tak obliczone bo ja nadal nie wiem:<<<

pyzia: blagam na kolankach o wytlumaczenie 🥺

pyzia: blagam na kolankach o wytlumaczenie 🥺

pyzia: blagam na kolankach o wytlumaczenie 🥺

wredulus_pospolitus: 1. Musisz wykazać, że trójkąt BOC jest prostokątny. 2. Wtedy można skorzystać ze wzoru na wysokość: https://matematykaszkolna.pl/strona/6391.html

#k: Srodek okręgu wpisanego w czworokąt leży na przecięciu się dwusiecznych katów . Kąt B i kąt C są to kąty przyległe . Dwusieczne kątów przyległych przecinają się pod kątem prostym .Stąd trójkąt BOC jest prostokątny . Natomiast r to wysokośc tego trójkąta