Zadanko na rozszerzenie nacix: Zadanko na rozszerzenie W czworościanie ABCS krawędzie AC,AS,BC,BS i CS mają tę samą długość równą 1. Oblicz, jaka powinna być długość krawędzi AB, aby objętość czworościanu była największa.

Tadeusz: .. jeśli wszystkie krawędzie boczne mają tą samą długość to spodek wysokości jest w środku okręgu opisanego na trójkącie podstawy. Dwa boki trójkąta podstawy też są równej długości zatem trójkąt ten jest równoramienny ... dalej ≥już dla Ciebie

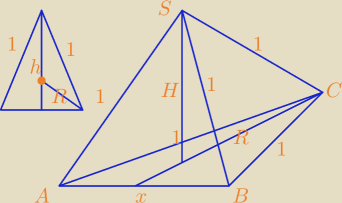
Godzio: Spodkiem wysokości jest środek okręgu opisanego na podstawie.

	1		1		1		1
(		x)2 + h2 = 12 ⇒ h2 = 1 −		x2 =		(4 − x2) ⇒ h =		√4 − x2
	2		4		4		2

	h * x		1   √4 − x2x 2		1
Pp =		=		=		x√4 − x2
	2		2		4

	a * b * c		1 * 1 * x		1
R =		=		=
	4P		1   4 * x√4 − x2   4		√4 − x2

R² + H² = 1²

	1		4 − x2 − 1		3 − x2
H2 = 1 −		=		=
	4 − x2		4 − x2		4 − x2

H = √(3 − x²)/(4 − x²)

	1		1		1
V =		* Pp * H =		*		x√4 − x2 * √(3 − x2)/(4 − x2)
	3		3		4

Ostatecznie:

	1
V(x) =		x√3 − x2
	12

Dziedzina: D = (0,√3) Szukamy x, dla którego objętość jest maksymalna,

	1		1		1
V'(x) =		√3 − x2 +		x *		* (−2x)
	12		12		2√3 − x2

	1		x2		3 − x2 − x2
V'(x) =		√3 − x2 −		=		=
	12		12√3 − x2		12√3 − x2

	3 − 2x2		3		√6
=		= 0 ⇒ x2 =		⇒ x =
	12√3 − x2		2		2

nacix: Dziękuję bardzo serdecznie !