ZW funkcji oraz jej szkic. Michał: Wyznacz dziedzinę, zbiór wartości, miejsca zerowe i naszkicuj wykres funkcji danej wzorem: y=x²−|x|+2 Mam obliczoną dziedzinę (R, mam nadzieję) oraz miejsca zerowe (Brak) nie mam pomysłu jak obliczyć zbiór wartości.

J: y = x² − x + 2 dla: x ≥ 0 y = x² + x + 2 dla: x < 0

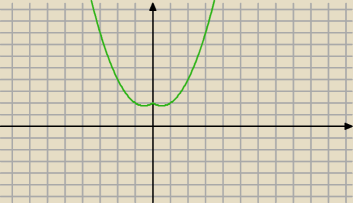
J: tutaj masz wykres

Michał: Dzięki wielkie. Ale chciałbym wiedzieć jak go samemu naszkicować. Oraz co opuszczenie modułu daje mi przy obliczeniu ZW?

J: patrz: 13:32 ... jak rysować

PW: Najskuteczniej byłoby zauważyć, że funkcja f(x) = x² − |x| + 2 jest parzysta, f(−x) = f(x), czyli wykres ma symetryczny względem osi OY. Wystarczy więc zająć się wykresem dla x ≥ 0, czyli wykresem funkcji f₁(x) = x² − x + 2, x∊<0,∞), a "drugą połowę wykresu" uzyskać jako symetryczny obraz wykresu funkcji f₁. Uwaga. Wierzchołek paraboli o równaniu g(x) = x² − x + 2

	7
należy do dziedziny funkcji f1 i ma rzędną yw =		− takie jest minimum f1, a więc i
	4

minimum f (badana funkcja osiąga to minimum w dwóch punktach:

	1		1
dla x =		i dla x = −		..
	2		2

PW: Korekta: Zamiast "wierzchołek paraboli o równaniu ( ... ) należy do dziedziny funkcji f₁" powinno być "wierzchołek (...) należy do wykresu funkcji f₁.

Michał: Dzięki wielkie!