 Przedstaw na plaszczyznie zespolonej zbior liczb zespolonych spelniajcych rownanie
Re(z+1)=Im(2z−4i)
nie mam za bardzo pomysłu jak się za to zabrać. Ale logicznie rzec biorac, na podstawie Re(z+1)
wychodzi mi, że x+1+yi, więc y=x+1 , a z drugiego Im(2z−4i) wychodzi mi, że y=−4 . Czyli to po
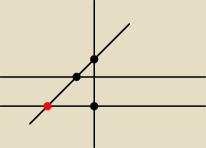
prostu będzie taki wykres?
Punkt czerwony oznacza czesc wspolna
Przedstaw na plaszczyznie zespolonej zbior liczb zespolonych spelniajcych rownanie
Re(z+1)=Im(2z−4i)
nie mam za bardzo pomysłu jak się za to zabrać. Ale logicznie rzec biorac, na podstawie Re(z+1)
wychodzi mi, że x+1+yi, więc y=x+1 , a z drugiego Im(2z−4i) wychodzi mi, że y=−4 . Czyli to po
prostu będzie taki wykres?
Punkt czerwony oznacza czesc wspolna
| 1 | 5 | |||
y = | x + | |||
| 2 | 2 |
| 1 | 5 | |||
Czyli w takim razie tym zbiorem liczb bedzie prosta o równaniu y= | x+ | ? | ||
| 2 | 2 |
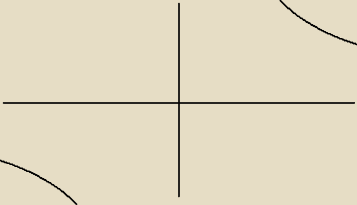 Dla Im(z2)≤8 zbiorem bedzie obszar miedzy hiperbola?
Dla Im(z2)≤8 zbiorem bedzie obszar miedzy hiperbola?

 To jeszcze jedno pytanie, mam nadzieję, że wybaczysz
To jeszcze jedno pytanie, mam nadzieję, że wybaczysz 
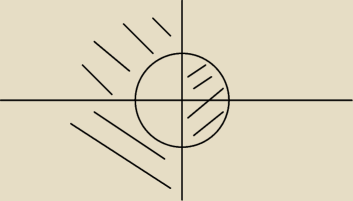
| 1 | ||
Dla Re( | )>Im(iz) wyszło mi, że dla | |
| z |