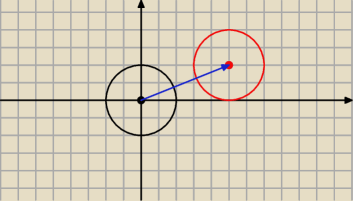
Okregi 5-latek: Cwiczenie nr 22. Sprawdz wzor (x−a)²+(y−b)² =r² dwoma sposobami przesuwając okrag o(0,r) o wektor OA =[a,b] i stosując bezpośrednio twierdzenia Pitagorasa do odpowiedniego trojkata prostokątnego którego przeciwprostokatna jest AP (=(x,y) dowolny '' bieżący'' punkt okręgu Nie lubie takich zadań

Mila: Dobranoc. Przeczytam jutro treść. Nie widziałam Cię dzisiaj, chory?

5-latek: Dobranoc Milu

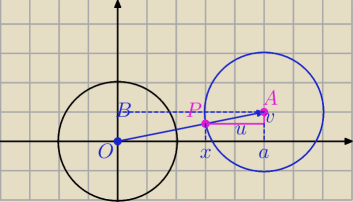
Mila: x²+y²=r² po translacji o niezerowy wektor otrzymujemy okrąg o tym samym promieniu. Zmienia się położenie. O=(0,0) O=(0,0)→T_[a,b]→A=(0+a,0+b)=A=(a,b) Równanie okręgu o środku A=(a,b) i promieniu r: (x−a)²+(y−b)²=r² II sposób: P=(x,y) u=|a−x| v=|b−y| |AP|²=r²=|a−x|²+|b−y|²⇔ (x−a)²+(y−b)²=r²

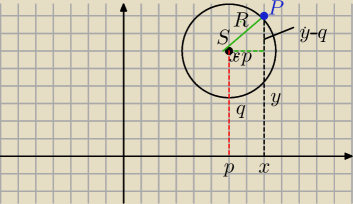
5-latek: Dobry wieczor Milu Pozdrawiam dziekuje CI bardzo . Wczoraj jeszcze znalazłem w książce Wlodzimierza Wrony Elementy rachunku wektorowego i geometrii analitycznej taki rysunek

5-latek: Zapomnialem dopisać √x−p)²+(y−q)²=R² lub inaczej (x−p)%2+(y−q)²=R²

Mila: To jest taka sama metoda jak moja, inny punkt okręgu wybrano.

5-latek: Milu To zauwazylem wlasnie