Wyznacz miarę kiciaa: Odcinki o długościach: 2√3, 3 − √3, 3√2 są bokami trójkąta. Wyznacz miarę największego kąta tego trójkąta. Wielkie dzięki za pomoc

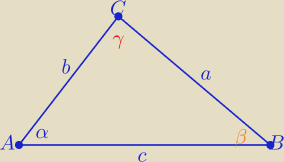
Eta: |AB|=c=3√2≈4,23 , |AC|=b=3−√3≈1,3 , |BC|=a=2√3≈3,46 to największym kątem jest kąt γ leżący na przeciw najdłuższego boku ( czyli boku c) z tw. kosinusów:

	b2+a2−c2		(3−√3)2+(2√3)2−(3√2)2
cosγ=		=
	2ab		2*(3−√3)*3√2

	1
cosγ= .............................. = −
	2

to γ= 120^o