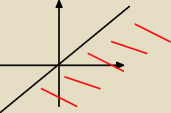
Zespolona, nierówność PakuS: Sprawdzi ktoś? Dla jakich liczb zespolonych zachodzi równość: Re(z)>Im(z) Wychodzi x>y Czyli rozwiązaniem jest wszystko pod prostą y=x. Czy tak? Pozdrawiam

J: tak

PakuS: Dzięki I jeszcze tak dla pewności Imz²<8 Wynik y<4?

J: nie ... 2xy < 8

PakuS: A Im nie odnosi się tylko do i?

J: tylko do i .... z² = (x+iy)² = x² + 2xyi − y² ... czyli: Imz² = 2xy

PakuS: Ok błąd w rachunkach

PakuS: A taki przypadek? _ |z|=z*z √x²+y²=(x²+y²)² i rozwiązaniem będzie 0 i x albo y = 1?

J: nie rozumiem prawej strony pierwszego równania

PakuS: moduł z = z razy sprzężenie z