wyznacz asymptoty Marta:

x3
	może mi ktoś podpowiedzieć jak mam wyznaczyć asymptoty, jeśli licząc granice, w
x2−9

liczniku sa wyższe potęgi niż w mianowniku?

Qulka: wykluczenia w dziedzinie to asymptoty pionowe jeśli w liczniku wykładnik potęgi jest dokładnie o 1 większy niż w mianowniku to wychodzi asymptota ukośna y=ax+b gdzie a=lim f(x)/x oraz b = lim f(x)−ax

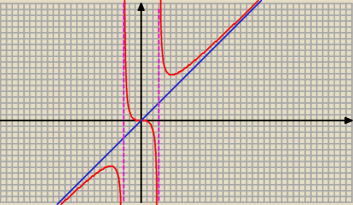
Janek191: Asymptoty poziome : x = − 3 , x = 3

f(x)		x3		x2		1
	=		=		=
x		x*(x2 − 9)		x2 − 9		1 − 9x2

więc

	f(x)
lim		= 1
	x

x→ −∞

	f(x)
lim		= 1
	x

x→+∞ a = 1

	x3		x3 − x*( x2 − 9)		9 x
( f(x) − a x) =		− x =		=		=
	x2 − 9		x2 − 9		x2 − 9

	9
=
	x − 9x

więc lim ( f(x) − x) = 0 x → 0 b = 0 Asymptota ukośna ma równanie y = a x + b, czyli y = x ====

Janek191: Na początku miało być oczywiście − asymptoty pionowe: x = − 3 oraz x = 3

Marta: dziękuję bardzo

Janek191: Poprawka Ma być lim ( f(x) − x) = 0 x → ∞