potrzebne na już! Bardzo prosze jozio: Z twierdzenia cosinusów W trójkącie ABC kąt przy wierzchołku A ma miarę 120 stopni. Długości boków tego trójkąta tworzą ciąg arytmetyczny. Oblicz AB/BC=AC/BC. (AB,BC,AC to długości boków. AB=√97 BC=√40 CA=√45

sushi_gg6397228: co to jest AB/BC = AC/BC ?

jozio: to co mam obliczyć. a to co jest poniżej to nie to zadanie, te długości to nie do tego, pomyliłem się.

sushi_gg6397228: to z tego zapisu AB= AC, a to oznacza ze trójkąt jest równoramienny rozwartokątny a taki nie moze być, bo boki maja tworzyć ciąg przepisz porządnie treść zadania

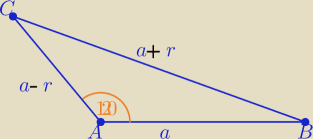
Eta: r∊(0,a) r>0 i a>0 cos120^o= −0,5

	(a−r)2+a2−(a+r)2		1
z tw. kosinusów cos120o=		=		/*2
	2a(a−r)		2

a2−4ar		5
	=1 ⇒ 2a2−5ar=0 |:a >0 ⇒ 2a−5r=0 ⇒ a=		r=2,5r
a(a−r)		2

|AB|=2,5r , |AC|=2,5r−r=1,5r , |BC|=2,5r+r= 3,5r to :

|AB|		|AC|
	= ............ i		=..........
|BC|		|BC|