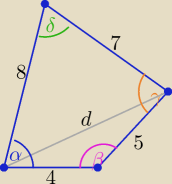
Z warunku opisania okręgu na czworokącie:
β+δ=α+γ=180o to δ= 180o−δ
cosδ=cos(180o−β)= − cosβ
z tw. kosinusów:
d2=42+52−2*4*5*cosβ i d2= 82+72−2*7*8*cosδ= 82+72+2*7*8*cosβ
porównaj obydwie strony tych równań to otrzymasz :
...............................
| 9 | ||
cosβ= − | ||
| 19 |