pochodne bombom: Wykorzystując warunek wystarczający z drugą pochodną wyznaczyć ekstrema funkcji.

	1
f(x) = x +
	x

wydaje mi sie, że mam policzyc pochodną:

	1
f'(x) = 1 +
	x2

i teraz pochodna 2 stopnia

	2x
f'(f'(x))=
	x4

i dalej nie mam pojecia jak zrobić. z góry dziękuje za pomoc!

Janek191: Źle policzona I pochodna

bombom: co z nią nie tak?

PW: Za bardzo pozytywna.

Janek191:

	1
f(x) = x +
	x

	1
f '(x) = 1 −		= 1 − x−2
	x2

	2
f ''(x) = − (−2) x−3 = 2 x−3 =
	x3

bombom: błąd we wzorze. A o co chodzi z tym warunkiem wystarczajacym?

Janek191:

	1
f '( x) = 0 ⇔ 1 −		= 0 ⇔ x = −1 lub x = 1
	x2

więc

	2
f ''( − 1) =		= − 2 < 0 − f ma maksimum lokalne dla x = − 1
	−1

	2
f ''(1) =		= 2 > 0 − f ma minimum lokalne dla x = 1
	1

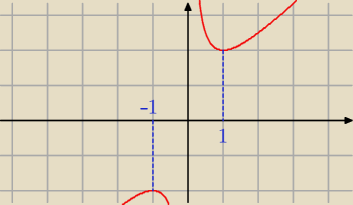
Patrz też wykres funkcji f

bombom: Dziękuje!