Proszę o pomoc
#60;M#62;: Sześcian i ostrosłup prawidłowy czworokątny mają w podstawie kwadrat o boku długości
10. Wiadomo, że objętość ostrosłupa jest równa objętości sześcianu.
a) Wyznacz wysokość ostrosłupa.
b) Oblicz pole powierzchni całkowitej ostrosłupa.
c) Wyznacz sinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
2. W graniastosłupie prawidłowym czworokątnym przekątna ściany bocznej ma długość 15
cm i tworzy z przekątną graniastosłupa, wychodzącą z tego samego wierzchołka, kąt 30°.
Oblicz objętość graniastosłupa oraz długość jego przekątnej.
3. Podstawą ostrosłupa jest trójkąt równoboczny o boku długości 3 cm. Spodek wysokości
ostrosłupa jest jednym z wierzchołków podstawy. Ściana boczna, która nie zawiera
wysokości ostrosłupa, jest nachylona do płaszczyzny podstawy pod kątem 45°. Oblicz:
a) wysokość ostrosłupa,
b) objętość ostrosłupa,
c) pole powierzchni całkowitej ostrosłupa,
d) sumę długości wszystkich krawędzi ostro
16 lis 16:49
dero2005:
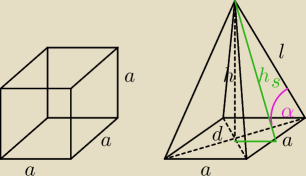
a = 10
V
p = V
o
h = 30
h
s =
√h2 + (a2)2 =
√302 + 52 = 5
√37
P
c = a
2 + 2ah
s = 100(1+
√37)
d = a
√2 = 10
√2
l =
√h2 + (d2)2 = 5
√38
16 lis 21:56
dero2005:
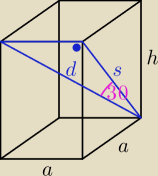
s = 15
a = 5
√3
h =
√s2 − a2 = 5
√6
V = a
2h = 375
√6
d =
√s2 + a2 = 10
√3
16 lis 22:07
dero2005:
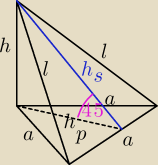
a = 3
| | a2√3 | | a*hs | |
Pc = |
| + a*h + |
| = dokończ |
| | 4 | | 2 | |
l =
√h2 + a2 = dokończ
S = 3a + 2l + h = dokończ
16 lis 22:19