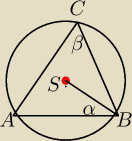
Okrąg opisany na trójkącie ostrokątnym. Krystek22: Muszę wykazać, że α + β = 90^o jeżeli S jest środkiem okręgu trójkąta opisanego na tym trójkącie ABC. Mógłby mi ktoś podpowiedzieć, dać jakąś wskazówkę jak to zrobić?

ror: S− środek okręgu opisanego na trójkącie ABC <ASB=2β trójkąt ASB jest równoramienny suma miar kątów wewnętrznych dowolnego trójkąta =180^o

Krystek22: Rozumiem, że ASB = 2β wzięło się z tego, iż kąt środkowy ma miarę dwukrotnie większą niż kąt wpisany oparty na tym samym łuku, tak? Ok, czyli mam ASB = 2β zatem w trójkącie ASB: α + α + 2β = 180^o ⇔ 2α + 2β = 180^o ⇔ α + β = 90^o c. n. d. Tak to mogę zapisać czy coś pominąłem?

ror:

Krystek22: Dzięki za pomoc.

ror: