zadanie na udowodnienie
kosek: wykaż że dla każdej liczby rzeczywistej x prawdziwa jest nierówność x2+1>2|x|
15 lis 23:28
zastanow sie:
podstaw np 1
15 lis 23:29
olekturbo: dla x ≥ 0
x2+1 > 2x
x2−2x+1 > 0
(x−1)2 > 0
Kwadrat liczby zawsze jest większy bądź równy zero.
dla x < 0
x2+1>−2x
x2+2x+1>0
(x+1)2>0
15 lis 23:31
kosek: musze to zrobic na literkch, a nie podstawiajac ..
15 lis 23:31
zastanow sie:
'badz rowny' − a ma byc wiekszy
15 lis 23:32
olekturbo: No bo jest jeszcze (−1)2 ... wystarczy dać odpowiednią adnotację.
15 lis 23:34
zastanow sie:
nie udowodnisz tego, bo dla −1 i 1 nierownosc nie jest spelniona.
15 lis 23:34
olekturbo: pokazalem jak wykazac nie jak uzasadnic
15 lis 23:34
olekturbo: Ahm. Pewnie autor chciał ≥.
15 lis 23:34
zastanow sie:
drogi kosek, myslenie logiczne w matematyce jest jak najbardziej wskazane. skoro istnieje
liczba rzeczywista (niezbyt trudna do odgadniecia) ktora nie spelnia zalozen to po co sie brac
za 'literki' ?
15 lis 23:37
Mila:
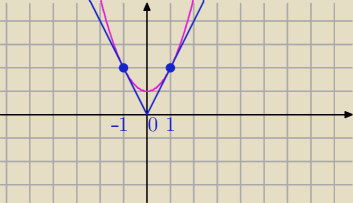
x
2+1
≥2|x|
15 lis 23:46
 x2+1≥2|x|
x2+1≥2|x|