Parametr piniondze: Dla jakich wartości parametru p równanie ma co najmniej trzy rozwiązania? |x²−6x+8|+|x²−6x+5|=p

piniondze: :c

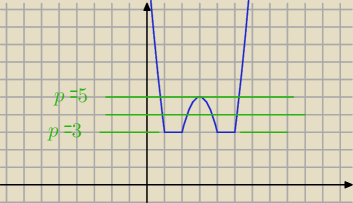
Qulka: dla p∊<3;5>

:): Jak nie wiesz jak, to zacznij od przypadków żeby opuścić wartość bezwględną zauważ, że jak podstawisz x−3=y to masz x²−6x=(x−3)²−9=y²−9 |y²−1|+|y²−4|=p

piniondze: no i potem przedziały co nie? I: x ∊ (−∞,−2) y²−1+y²−4=p 2y²−5=p y=√ ^{p + 5} ₂ x−3 =√ ^{p + 5} ₂ x=√ ^{p + 5} ₂ +3 i co dalej?

piniondze: w sumie metoda graficzna w tym przypadku jest o wiele szybsza xd

piniondze: no ale nie zawsze da sie graficznie.

:): żeby zrobić metodą graficzną trzeba wiedzieć jak wyglada wykres... Tu zrobił to program, a ty i tak musisz przedziałami

piniondze: to co mam zrobic dalej z tamtym wyrazeniem? √^{p + 5}₂<−2 i to rozwiązać?

:): f(x)=|x²−6x+8|+|x²−x+5| rozpatrz przypadki, zeby pozbyć się wartości bezwględnej.. w efekcie będziesz wiedział jak wygląda wykres f i wtedy już jak Qulka. (tak to skąd masz wiedzieć jak narysować tą niebieską linie )

piniondze: no można sobie spróbować jakoś poskładać te wykresy, zrobić dwie tabele i dodawać po chłopsku xd

Qulka: i tak jak w tabelkach, tak w przedziałach.. nie mieszać do tego p

Mila: f(x)=|x²−6x+8|+|x²−6x+5| ładny jest wykres , więc rozpisałam wzór w przedziałach : 1) f(x)=2x²−12x+13 dla x∊(−∞,1>lub x∊<5,∞) x_w poza przedziałami (i dobrze ) 2) f(x) =3 dla x∊(1,2>lub x∊<4,5) 3) f(x)=−2x²+12x−13 dla x∊(2,4) x_w=3,y_w=5 spróbuj dokończyć, gdy sobie to wszystko przeliczysz i narysujesz.

PW: Warto zauważyć, że funkcje "między kreseczkami" różnią się o 3, jeżeli więc x² − 6x + 5 ≥ 0, czyli gdy x∊(−∞,1>∪<5,∞), to również x² − 6x + 8 > 0 i wtedy równanie przyjmuje postać (1) 2(x² − 6x + 5) + 3 = p, x∊(−∞,1>∪<5,∞). Jeżeli x² − 6x + 8 < 0. czyli gdy x∊(2, 4), to również x² − 6x + 5 < 0 i wtedy równanie przyjmuje postać (2) −2(x² − 6x +5) − 3 = p, x∊(2, 4). Na pozostałej części osi, to znaczy na zbiorze (1, 2>∪<4, 5) rozważane funkcje kwadratowe mają różne znaki i równanie przyjmuje postać x²−6x+8 − x²+6x −5 = p, x∊(1, 2>∪<4, 5) (3) 3 = p, x∊(1, 2>∪<4, 5). Zadane równanie jest więc alternatywą trzech równań na trzech podzbiorach osi: (1) lub (2) lub (3). Każde z tych równań może mieć swoje rozwiązania w zależności od parametru p. Naszym zadaniem jest tak dobrać p, aby w sumie były co najmniej 3 rozwiązania. Warto to wszystko rysować (lewe strony równań są pewnymi funkcjami zmiennej x, w szczególności lewa strona (3) jest funkcją stałą zmiennej x). Wykonanie dobrego rysunku wszystkich trzech funkcji w jednym układzie współrzędnych pozwoli zobaczyć odpowiedź, gdy przetniemy wykresy prostą y = p.

Eta:

PW: Grzebałem się, ale chyba to co napisałem jest opisem do rysunku Qulki

piniondze: OOOO! DZIĘKI WIELKIE

piniondze: No tak wychodzi, ale przynajmniej teraz wiem jak się wgl do takiego czegoś zabrać.