kat pod jakim przecinaja sie wykresy dwoch funkcji
.: oblicz kat pod jakim przcinaja sie wykresy dwoch funkcji:
f(x)=sin x
g(x)= sin (x+π/4)
15 lis 19:00
.: Jest jakis wzor ktory mogl bym uzyc do tego zadania


15 lis 19:13
.: Ktos pomoze ?
15 lis 19:42
Janek191:
Znajdź punkt wspólny wykresów tych funkcji, równania stycznych do tych funkcji
w danym punkcie, tg kąta między tymi prostymi

15 lis 19:44
Janek191:
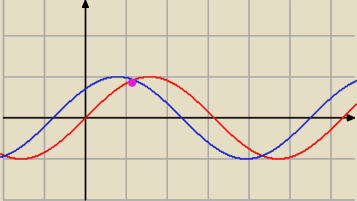
15 lis 19:47
.: Juz mam punkty wspolne (3π/8) i (11π/8)
15 lis 19:56
.: Obliczylem takze pochodne funkcji f(x) i g(x):
f'(x)= cos x
g'(x)= cos(x+π/4)
15 lis 19:57
.: Teraz jak obliczyc ten kat?
15 lis 19:58
Janek191:
| | 3π | |
a1 = f '( |
| ) = ... = tg α |
| | 8 | |
| | 3π | |
a2 = g '( |
| ) = ... tg β |
| | 8 | |
oraz
| | tgα − tg β | |
tg γ = tg ( α − β) = |
| |
| | 1 + tg α*tg β | |
15 lis 20:15
.: ok, to:
tg α = (√2−√2)/2
tg β = −(√2−√2)/2
15 lis 20:25
.: czy α = 41.88 to poprawna odpowiedz ?
15 lis 20:57
.: tg α − tg β = √2−√2
1+ tg α * tg β = 1−(2−√2)/4 = (2+√2)/4
tg γ = (4√2−√2)/(2+√2)
γ = tg−1(tg γ)
γ= 41.88
Zgadza sie ?
16 lis 19:44



