Planimetria Metis: Obliczyć długości x, y, z http://prntscr.com/92ztp4 Jakiś pomysł ? Sprawdźcie przy okazji czy dobrze obliczyłem szukana odcinek x. Mam nadzieje, że rysunek czytelny

Metis:

Kacper: Szukaj w odpowiedziach

Metis: Zad 7. http://www.diament.agh.edu.pl/images/dokumenty/matematyka_II_2014_2015.pdf W trójkąt prostokątny o przyprostokątnych a = 15 cm, b = 20 cm wpisany jest okrąg. Oblicz odległości od każdego wierzchołka trójkąta do punktu styczności okręgu z przeciwległym bokiem.

Metis: Coś źle mi to wyszło.

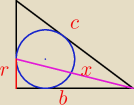
Aga1.: c=√225+400=25

	a+b−c
r=		=10
	2

x=√10²+20²=10√5

Metis: Dzięki Aga1 , własnie sie zorientowałem że mam zły rysunek... Dwa razy Pitagoras potem z tw Cosinusow i wyjdzie.

Aga1.: Nie, r=5, zatem x też źle.

Metis: x=5√17

Aga1.: tak.

Kacper: Marzy ci się startować ?

Metis:

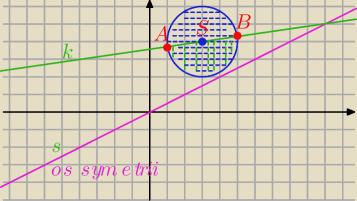
Metis: Wytłumaczy mi ktoś zadanie 5? Pierwszy raz spotykam się z takim zadaniem. Szukałem w książkach pod tematem wielomian kilku zmiennych, ale nie ma interpretacji geometrycznej. Ewentualnie jakieś linki dot takich zadań. Treść: Figura B jest obrazem figury A = {(x, y) : x² + y² − 6x − 8y + 21 ≤ 0 ∧ x − 7y + 25 ≥ 0}. przez symetrię względem prostej x − 2y = 0. Znajdź nierówności opisujące figurę B i oblicz jej obwód.

Mila: Podpowiedź: 1) Napisz równanie kanoniczne okręgu

Metis: (x−a)²+(y−b)²=r² x²−6x+y²−8y+21≤ 0 x²−6x+9+y²−8y+16−4≤0 (x−3)²+(y−4)²−4≤0 (x−3)²+(y−4)²≤4

Metis: Otrzymałem równanie koła

Metis: S=(3,4) , r=2

Mila: Druga podpowiedź: A = {(x, y) : x² + y² − 6x − 8y + 21 ≤ 0 ∧ x − 7y + 25 ≥ 0}. x−7y+25≥0⇔x+25≥7y⇔

	1		25		1		25
y≤		x+		obszar na prostej y=		x+		i poniżej prostej tej prostej.
	7		7		7		7

x² + y² − 6x − 8y + 21 ≤ 0⇔ (x−3)²+(y−4)²≤2² koło o S=(3,4) i r=2 B − część wspólna , sprawdzamy czy S∊prostej k

	1		25		28
y=		*3+		=		=4, tak , należy, zatem
	7		7		7

B jest półkolem poniżej prostej k. Symetria nie zmienia wielkości, tylko położenie . Obwód półkola: 2*2+π*2=4+2π 2) Obraz w symetrii, Znajdź wsp. A i B. Znajdź punkty symetryczne do A,B względem prostej s.

Metis: Dziękuje Milu, analizuję

Metis: Zatem punkty przeciecia znajdę rozwiązując układ równan: |(x−3)²+(y−4)²=2² | x − 7y + 25= 0 Symetryczne potem bez problemu.

Mila: Tak.

Metis: Ze znalezionych punktów względem danej prostej wyznaczę równanie koła, a szukane półkole ogarnicze obszarem , analogicznie jak w figurze A. Serdecznie dziękuje Milu

Mila: Równanie koła bardzo prosto: S' jest środkiem odcinka A' B', r=2.

Metis: Oczywiście w poście 17:22 , z pośpiechu napisałem równanie koła, poprawnie: nierówność koła