Dla zbiorów, oblicz: Helios: Dla zbiorów C i D oblicz: C\D

	x + 1		x − 1
C:		< 1 D:		< 0
	x − 1		x2 − 3

J: na początek wyznacz zbiory: C i D

Helios: C: x+1 < x−1 i tutaj napotykam największy problem, bo lewa strona zeruje mi się z prawą, więc C=R ? D: x−1 < 0 x < 1 D: (−∞, 1)

J: tak nie wolno ...

	x+1
C : ⇔		− 1 < 0 ... i wspólny mianownik
	x−1

Helios:

x + 1		x − 1		2
	−		=		< 0
x − 1		x − 1		x− 1

J: tak

Helios: A czy zbiór D został wyznaczony odpowiednio?

J: D: (x−1)(x + √3)(x−√3) < 0

Helios: W jaki sposob (x−1) został ściągnięty z kreski ułamkowej?

J:

a
	< 0 ⇔ a*b < 0
b

Helios: Czyli to samo prawo mogę zastosować w wyznaczeniu x ze zbioru C?

J: tak ... ⇔ x − 1 < 0

Helios: Ok, zbiór C już rozumiem. A jak wyznaczyć x ze zbioru D?

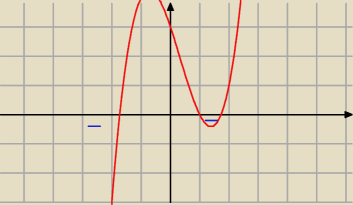
Aga1.: D=(−∞,−√3)U(1,√3)

Helios: W odpowiedziach zawarta jest taka odpowiedź: x∊(−1;∞)

Helios: i coś mi tu nie gra..

Aga1.: To może inna nierówność?

Helios: W jakim sensie? Nie rozumiem...

Aga1.: Sprawdź wszystko po kolei, czy dobrze przepisałeś z książki

Helios: Wszystko z książki przepisałem dokładnie. Więc jak rozumiem, gdzieś jest błąd w książce. To całkiem możliwe, bo już kilka znalazłem.

Helios: Mimo wszystko, wielkie dzięki za pomoc