Kwadrat Krzysiek: Na bokach BC i CD kwadratu ABCD wybrano takie punkty E i F, że miara kąta EAF jest równa 45 stopni. Odcinki AE oraz AF przecinają przekątną BD kwadratu odpowiednio w punktach G i H. Wykaż, że pole trójkąta AGH jest równe polu czworokąta GEFH.

Tymon: ?

Tymo:

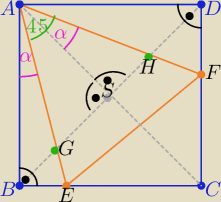
Eta: 1/ |<BAE|=|<HAS|=α 2/ ΔABS jest prostokątny i równoramienny to |AB|=|AS|*√2

	|AB|
zatem:		= √2
	|AS|

3/ trójkaty ABE i HAS ( prostokątne) i są podobne z cechy (kkk)

	|AE|
to:		=U{|AB|}{{|AS|}= √2 = k −− skala podobieństwa
	|AH|

4/ analogicznie trójkąty ADF i AGS są podobne z cechy (kkk)

	|AF|		|AD|		|AB|
to:		=		=		=√2
	|AG|		|AS|		|AS|

5/ to i podobne są trójkąty EFA i GHA z cechy ( bkb) bo U{|AE|}{|{AG|}=U{|AF|}{{AH|}= √2 =k −−−skala podobieństwa zatem

P(ΔEFA)
	=k2=2 ⇒ P(AEF)=2P(AGH)
P(ΔGHA)

i mamy tezę : P(GEFH)=P(AGH) c.n.u

Eta: Poprawiam zapis :

	|AE|		|AF|
5/ ... bo		=		=√2=k −−− skala podobieństwa
	|AG|		|AH|

Eta: I co Tymon? żyjesz?

Tymon: Nie rozumiem tego