Prosze o pomoc , bo nw jak sie za to zabrać
Lotnik: Jakie jest prawdopodobienstwo, ze pierwiastki równania x2 + 2bx + c = 0 sa rzeczywiste,
jesli liczby b i c zostały wybrane losowo z przedziału [0, 1]?
13 lis 17:58
Lotnik: Pomoże ktoś

?
13 lis 18:04
===:
... to może "przerysuj" treść tego zadania. W matematyce już dawno przed Tobą
przyjęto zasadę jak oznaczamy przedziały

13 lis 18:08
Lotnik: Jakie jest prawdopodobieństwo , że pierwiastki równania x2+2bx+c=0 są rzeczywiste, jeśli
liczby b i c zostały wybrane losowo z przedziału [0,1]?
13 lis 18:15
ICSP: warunek na to aby pierwiastki były rzeczywiste ?
13 lis 18:36
Lotnik: Δ>0 ?
13 lis 18:44
ICSP: prawie. Tak czy inaczej trzeba liczyc wyróżnik. Potem wykonać odpowiedni rysunek i za pomocą
całki policzyć pole.
13 lis 18:45
Lotnik: a co jak nie miałam ccałek i nie bardzo sie orientuje jak ?
13 lis 18:48
ICSP: Nie mam pomysłu jak to bez całek zrobić.
13 lis 18:55
Lotnik: a mogłabym prosić o rozwiązanie z całkami ?
13 lis 18:56
ICSP: skoro nie miałaś jeszcze całek to i nie zrozumiesz tego rozwiazania.
13 lis 19:02
Lotnik: no ale może znajde kogoś kto mi wytłumaczy
13 lis 19:05
ICSP:
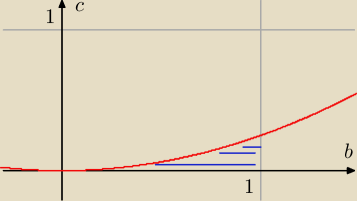
|Ω| = 1
13 lis 19:17
ICSP: ale niech ktoś to lepiej sprawdzi jeszcze

13 lis 19:18
Lotnik: no własnie w odpowiedziach jest 13
13 lis 20:01
ICSP: | | 1 | |
ano faktycznie będzie |
| . |
| | 2 | |
D(p) = 4b
2 − 4c > 0 ⇒ b
2 > c
Nie widziałem dwójki stojacej przy b.
13 lis 20:04
ror: delta źle obliczona
13 lis 20:04
ror: o teraz ok
13 lis 20:04
Lotnik: super dziękuje

teraz bede sie meczyc z tymi całkami moze cos zrozumiem
13 lis 20:05
 ?
?



 teraz bede sie meczyc z tymi całkami moze cos zrozumiem
teraz bede sie meczyc z tymi całkami moze cos zrozumiem