równanie kwadratowe z wartością bezwzględnął i parametrem janczar: Dla jakich wartości parametru m równanie x²− (m+1)|X|+1=0 ma cztery różne rozwiązania . wiem że delta musi być > 0. Dalej Zupełnie nie wiem jak sie za to zabarać doszedłem dpo tego ,że trzeba za |x| podstawiać t i ,że delta wynosi m² + 2m − 3 jednak nie wiem co dalej . Proszę o rozwiązanie algebraiczne i wytłumaczenie . z góry dziękuję

PW: Popełniasz na samym wstępie podstawowy błąd. Jaka delta? Przecież to nie jest równanie kwadratowe. Już w samym zadaniu wyraźnie to sugerują (równanie kwadratowe może mieć co najwyżej dwa rozwiązania, a tu mówią o czterech).

janczar: Jest wartość bezwzgledna wiec może być 4 róże. P.s jakie to wg cb rozwiazanie

PW: Proszę, nie dyskutuj z podstawowymi faktami, i nie tłumacz mi tego co się wytłumaczyć nie da. Przy poszukiwaniu rozwiązania pomijamy x = 0, które rozwiązaniem nie jest. Zadane równanie dla pozostałych x jest alternatywą dwóch równań − jedno ma postać (1) x² − (m+1)x + 1 = 0, x∊(0,∞), drugie (2) x² − (m+1)(−x) + 1 = 0, x∊(−∞, 0). W ten sposób można znaleźć warunek na istnienie czterech rozwiązań − dwa dla równania (1) i dwa dla równania (2). Można też inteligentnie: zauważyć, że zadane równanie ma symetryczne rozwiązania (jeżeli liczba x₁ jest rozwiązaniem, to także liczba − x₁ jest rozwiązaniem). Wystarczy więc tak dobrać parametr m, aby równanie (1) miało dwa rozwiązania dodatnie x₁ i x₂.

===: ... a Ty janczar podyskutuj z tymi "jedynie słusznymi faktami" Skoro a>0 i c=1 to warunkiem istnienia czterech pierwiastków jest y_w<0

	−Δ
zatem		<0 .... i baw się ta deltą (Zauważ, że znak przy b nie ma wpływu na Δ)
	4a

janczar: Pw jak podasz mi maila to wrzucę ci zdj książki . To zadanie umieszczone jest w dziale f.kwadratowa z wart bezwzgledna i parametrem . Wybaczcie , ale dalej nie wiem za bardzo o co chodzi .

sushi_gg6397228: czytaj jeszcze raz post z 18.01; do momentu aż zatrybisz

Aga1.: Równanie 1) ma dwa różne rozwiązania dodatnie, gdy a) Δ>0⇒[−(m+1)}²−4>0 dokończ

	−b
b)x1+x2=		>0⇒m+1>0
	a

	c
c) x1*x2=		>0
	a

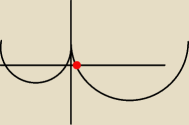
janczar: (1) x2 − (m+1)x + 1 = 0, x∊(0,∞), drugie (2) x2 − (m+1)(−x) + 1 = 0, x∊(−∞, 0). rozumiem ,że to rozważanie przez przypadki. Dlaczego więc nie ma tam tego minusa (2) − x2 − (m+1)(−x) + 1 = 0, x∊(−∞, 0). A czy nie można było by rozwiąząć tego zadania w ten sposób , że ustalam warunki jakie są potrzebne aby ta funkcja miała 4 rozwiązania a mianowice Δ<0 x1<x2 x1>0 , dla tych warunków mielibyśm taki wykresbyłby on symetryczne nie jak umnie na rysunku, nie umiem używac tego programu ) czerowna kropka to x1 przykłądowy

janczar: pozatym zauważ PW ,że delta wynmosi zero w obydwuch przypadkach

Metis: Jak ty liczysz tę deltę ?

janczar: b² −4ac = [−(m+1)]²−4*1*1 . Faktycznie masz racje zapomniałem odjąć 4 . Mój błąd

Metis: "aby ta funkcja miała 4 rozwiązania a mianowice Δ<0 x1<x2 x1>0 " − głupoty piszesz Przeczytaj uważnie post PW Wszystko masz tam napisane. Jeśli nie umiesz zrobić tego umiejętnie to rozpatruj kazde otrzymane równanie ( po opuszczeniu modułu) osobno!

Mila: x²− (m+1)|x|+1=0 1)x≥0 wtedy masz równanie: x²−(m+1)x+1=0 ma dwa różne dodatnie ( bo x nieujemne) rozwiązania dla : a) Δ>0 b) x₁+x₂>0 c) x₁*x_>0 Δ=(m+1)²−4>0 m²+2m−3>0 Δ_m=4+12=16

	−2−4
m=		=−3 lub m=1
	2

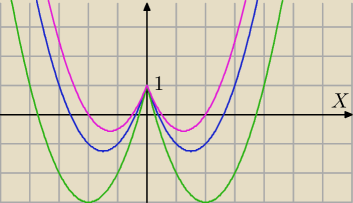
Δ>0⇔m<−3 lub m>1 x₁*x₂=1 niezależnie od wyboru m x₁+x₂=m+1 m+1>0 m>−1 Z (a),(b), (c)⇒ m∊(1,∞) 2) x<0 x²+(m+1)x+1=0 a) Δ>0⇔m<−3 lub m>1 b) x₁+x₂<0 c) x₁*x₂>0 dla m∊R x₁+x₂=−(m+1) −(m+1)<0⇔ m+1>0 m>−1 Z (a),(b), (c)⇒ m∊(1,∞) Przykłady masz na wykresie. Wyciągaj wnioski.

Eta: x²−(m+1)*|x|+1=0 −−− ma mieć 4 rozwiązania |x|²−(m+1)*|x|+1=0 podstawienie : |x|=t , t>0 ( bo dla x=0 równanie jest sprzeczne) t²−(m+1)t+1=0 −− to równanie musi mieć dwa dodatnie rozwiązania 1/Δ>0 ⇒ Δ= m²+2m−3 = ( m+3)(m−1) >0 ⇒ m∊(−∞,−3)U (1,∞) ze wzorów Viete^'a i 2/ t₁+t₂>0 ⇒ m+1>0 ⇒ m>−1 i 3/ t₁*t₂>0 ⇒ 3m²>0 ⇒ m>0 część wspólna powyższych warunków daje odpowiedź: Dla m∊( 1,∞) równanie ma cztery różne rozwiązania ze względu na zmienną "x"

Mila:

	c
t1*t2=		=1>0
	a

Eta: No jasne c= 1 a nie 3m² ( nie wiem skąd to zobaczyłam

5-latek: Mysle ze po π