hehe młodzik:

	x+2
(x2+4x)(x+2)−16*		≥0
	x2+4x

M:

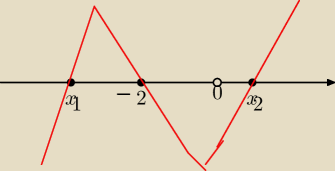Qiao Yunshu: Załozenie x≠0 lub x≠−4 (x²+4x)²(x+2)−16(x+2)≥0 (x⁴+8x³+16x²)(x+2)−16x−32≥0 x⁵+10x⁴+32x³+32x²−16x−32≥0 W(x)=x⁵+10x⁴+32x³+32x²−16x−32 W(−2)=0 (x⁵+10x⁴+32x³+32x²−16x−32)/(x+2)=x⁴+8x³+16x²−16 W(−2)=0 (x⁴+8x³+16x²−16)/(x+2)=x³+6x²+4x−8 w(−2)=0 x³+6x²+4x−8)/(x+2)=x²+4x−4 x²+4x−4=0 Δ=32=4√2

	−4−4√2
x1=		=−2−2√2≈−4,828
	2

x²=2√2−2≈0,828 x⁵+10x⁴+32x³+32x²−16x−32=(x+2)³(x−(−2−2√2))(x−(2√2−2)≥0 dla x∊[−2−2√2.−2]\{−4}U[2√2−2,∞) Tylko dużo rachunków jest

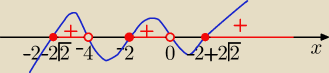
η: Nierówności tak mnożyć nie można Mnożymy przez kwadrat mianownika czyli tutaj przez (x²+4x)² zał. x≠0 i x≠ −4 mnożąc przez kwadrat mianownika otrzymujemy nierówność równoważną (x²+4x)³(x+2)−16(x+2)(x²+4x)≥0 (x²+4x)(x+2)[(x²+4x)²−16] ≥0 x(x+4)(x+2)(x²+4x+4)(x²+4x−4)≥0 x(x+4(x+2)³[(x+2)²−8]≥0 x(x+4)(x+2)³(x+2+2√2)(x+2−2√2)≥0 Odp: x∊[−2−2√2; −4) U [−2;0)U[−2+2√2;∞) =================================

Li Mo : W sumie to pomnozyłem przez kwadrat mianownika A że tak napisałem to juz inny temat