trygonometria ***tryg***: 479. wylicz x, dokończ rowiązanie: sinx=1 v sinx=−0,5

Godzio: sinx=1

	π
x=		+ 2kπ
	2

	1
sinx=−
	2

	π		π
x=−		+2kπ v x=π−		+2kπ
	6		6

	7π
x=		+2kπ
	6

AS: W drugiej części błąd i trochę brak konsekwencji

	π		π		5π
x = −		+2kπ v −π +		= −		+ 2kπ , k ∊ C
	6		6		6

lub

	π		7π		π		11π
x = π +		=		+ 2kπ v 2π −		=		+ 2kπ
	6		6		6		6

Godzio: rozwiązanie jest poprawne tyle że minusa zjadłem, ale go uwzględniłem x=−U{π}[6} +2kπ v x=π−(−U{π]{6}) +2kπ

	7π
x=		+2kπ
	6

AS: Ok.

***tryg***: a teraz prosiłabym o skończenie czegoś takiego:

	√3
2sinxcosx=
	2

tryg: wie ktoś jak takie coś rozwiązać? czy mam zamienić wszystko na jedna funkcję tryg... ale co to da, co dalej robić?

AS: Zastąpić 2sinxcosx wzorem sin2x

kaz:

	√3
2sinxcosx=sin2x=
	2

	π		π
2x=		+2kπ⋁2x=π−		+2kπ
	3		3

	π		π
x=		+kπ⋁x=		+kπ
	6		3

tryg: dziękuję, a teraz mam następne równanie. tym razem nie umiem go zupełnie zrobić. proszę o pomoc. 482. (cosx−sinx)²+tgx=2sin²x zaczęłam tak:

	π
zał: cosx≠o x≠		+kπ
	2

	sinx
rozw: cos2x−2sinxcosx+		−2sin2x=0
	cosx

	sinx
cos2x−sin2x−2sinxcosx+		=0
	cosx

	sinx
cos2x−sin2x+		=0... i nie wiem co dalej
	cosx

tryg: tam mi się wkradła pomyłka w linijce "rozw:

	sinx
cos2x−2sinccosx+sin2x+		−2sin2x=0
	cosx

Godzio: troche inaczej

	sinx
cos2x − 2cosxsinx +sin2 +		= 2sin2x /*cosx
	cosx

cosx − 2cos²xsinx +sinx = 2sin²xcosx 2cos²xsinx+2sin²xcosx=cosx+sinx 2sinxcosx( cosx +sinx)=cosx+sinx 2sinxcosx = 1 sin2x=1

Godzio:

	π
2x=		+2kπ
	2

	π
x=		+kπ
	4

AS: Szukałem sposobu na rozwiązanie zadania. Perspektywy pesymistyczne. Uzyskałem złożone równanie stopnia 6−go. Praktycznie nie do rozwiązania.

tryg: Godzio zupełnie nie rozumiem Twojego rozw. w momencie kiedy obustronnie mnożysz przez cosx Wg mnie powinieneś wtedy otrzymać coś takiego: cos³x−2cos²xsinx+sin²xcosx+sinx=2sin²xcosx możesz wyjaśnić?

kaz: ale cos²x+sin²x=1

Godzio: prócz tego momentu reszte rozumiesz ?

Godzio: (cosx+sinx) = cos²x + sin²x +sinxcosx =1 +sinxcosx ominąłem to żeby zaoszczędzić czasu

tryg: zrozumiałam a nawet zrobiłam troszke inaczej, po swojemu dziekuję bardzo. teraz następne, którego nie umiem 483. rozwiąż równanie: (1−tgx)(1+sin2x)=1+tgx

	π
zał: cosx≠0⇔x≠		+kπ
	2

Godzio: jaka jest odpowiedź bo wyszło mi coś ale, nie chce mi sie przepisywać skoro będzie źle

tryg: przepraszam, że dopiero teraz odp do 483. (1−tgx)(1+sin2x)=1+tgx

	π
x=−		+kπ lub x=kπ, k∊ℂ
	4

Godzio:

	sinx
1+sin2x − tgx −		* 2sinxcosx = 1+tgx /−1 / +tgx
	cosx

sin2x − 2sin²x = 2tgx /*cosx 2sinxcos²x − 2sin²xcosx = 2sinx 2sinxcos²x − 2sin²xcosx − 2sinx=0 sinx(2cos²x − 2sinxcosx−2) =0 sinx=0 x=kπ 2cos²x −2sinxcos − 2sin²x − 2cos²x=0 −2sinxcosx−2sin²x=0 /:(−2) sinx(cosx+sinx) =0 sinx=0 v cosx + sinx =0 cosx=sin(x+π/2)

	π
sin(x+		) = sin(−x)
	2

	π		π
x+		=−x+2kπ v x+		=π−(−x)+2kπ
	2		2

	π		π
x=−		+kπ v 0 =		+2kπ sprzeczne
	4		2

tryg: nie umiem tez jeszcze jednego. nie chcę tworzyć nowego tematu. licze na pomoc w obu przykładach. pozdrawiam i dziękuję rozwiąż równanie:

1−cos8x
	=0
1+tgx

	1
źle mi wychodzi, nie wiem jak zrobić poprawnie. w odpowiedziach jest: x=kπ lub x=		π+kπ, a
	4

wskazówka to: określ dziedzinę równania... określam więc: 1+tgx≠0 i tgx≠0

kaz: tgx≠−1

Godzio: tgx≠−1

	π
x≠−		+kπ
	4

	π		π
D: x≠−		+kπ i x≠		+kπ
	4		2

skoro tak to mamy równanie 1−cos8x = 0 cos8x = 1 8x=2kπ

	πk
x=
	4

	π		π
x≠−		+kπ x=		k
	4		4

spróbuj teraz bo nie określiłeś do końca dziedziny

tryg: Godzio, właśnie dokładnie tak napisaam na kartce jak Ty tutaj, tylko nie chciało mi się przepisywać. Nie zmienia to faktu, że w odpowiedziach napisali w innej postaci albo w ogóle coś innego. Podałam powyżej wyniki z książki. Proszę albo o dokończenie rozumowania albo jakieś wyjaśniania.

tryg:

	π
podtrzymuję pytanie do Godzia. Mam jeszcze jedno pytanie. odp do zadania ma być: x=		lub
	2

	3
x=π lub x=		π
	2

a tu jego treść: równanie sin2x=cosx+IcosxI wiedząc, że x∊<0,2π> ja robię tak: I cosx≥0 sin2x=2cosx 2sinxcosx−2cosx=0 2cosx(sinx−1)=0 cosx=0 v sinx=1

	π		π
x=		+kπ x=		+2kπ
	2		2

k∊ℂ₊ k∊ℂ₊ v II cosx<0 sin2x=0

	kπ
x=		, k∊ℂ−
	2

	π		3
czyli razem: x=		, x=		π bo k jest całkowite, podstawiam więc k=1, k=2... większe k
	2		2

powodują że x nie należy do wskazanego przedziału. [P[tylko skąd im się wzięło w odpowiedziach π]]?

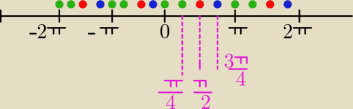
Godzio: to może zaznacze to na osi będzie lepiej widoczne

	π		π
czerwone(		+kπ) i niebieskie(−		+kπ) => nie spełnia
	2		4

zielone => spełnia odczytujemy:

	π
x=kπ v x=		+kπ
	4

tryg:

	π
moim zdaniem z drugiego przypadku można by otrzymać −π, −		tylko czemu tego nie zawarli w
	2

odpowiedziach?

Godzio:

	kπ
x=		k=1 v k=2 v k=3
	2

	π		3
x=		v x=π v x=		π
	2		2

Godzio: ale musisz patrzyć na przedział który "zakazuje" odpowiedzi ujemnych i większych od 2π

tryg:

	−π
a skąd Godzi bierzesz		?
	4

Godzio: Gdzie ?

tryg: ok, dziękuję, rozumiem wszystko z tego zadania pozdrawiam.

tryg: to było do tamtych kropeczek (niebieskich)

Godzio: no to dobrze

tryg: jednak mam pytanie do tego zadania. Gdy rozwiązywałam u góry to założyłam że II cosx<0 sin2x=0

	kπ
x=		, k∊ℂ− , moim zdaniem k musi być ujemne,
	2

	π		3
bo cos		, π ,		π wychodzi dodatni i to by się z kolei nie zgadzało z założeniem do
	2		2

przypadku. Z drugiej strony, te same wartości tylko ujemne nie należały by do wskazanego przedziału <0,2π>... i tu leży mój problem.

tryg: teraz mam jeszcze lepsze zadanie... pierwsze w zasadzie za które NIE WIEM jak się wziąć. próbowałam z logarytmów (żeby coś z tym 2 zrobić) ale nie poszło... rozwiąż równanie 3^sin2x=3^cos2x+2

Godzio: co do tamtego jeśli cosx < 0 to można zrobić tak: my rozpatrujemy x ale jeśli się narysuje w jednym układzie cosx i sinx to otrzymamy takie coś że: zapisuje to tylko dla przedziału <0,π> sinx > 0 w przedziale <0,π> później jest już ujemny cosx>0 w przedziale <0,π/2> potem jest już ujemny czyli nasze rozwiązanie znajduje się od π/2 do π

tryg: załapałam, dzięki wielkie. ponawiam prośbę o rozwiązanie: 3^sin2x=3^cos2x+2

Godzio: chętnie bym pomógł ale tego typu zadania mam przewidziane w mojej książce na trche później

Godzio: tak na chłopski rozum : 3^sin2x = 3^1−sin2x +2 3^sin2x = 3 : 3^sin2x +2 /*3^sin2x 3⁰ = 3 +2* 3^sin2x /−3 / :2 −1 = 3^sin2x a dalej nie wiem

Godzio: a nie czekaj i tak sie pomyliłem lepiej sie nie brać

Bogdan: 3^sin2x = 3^1−sin2x + 2 albo 3^1−cos2x = 3^cos2x + 2

Bogdan: 3^sin2x = 3^1−sin2x + 2

	3
3sin2x =		+ 2 / * 3sin2x
	3sin2x

3^2sin2x = 3 + 2*3^sin2x 3^2sin2x − 2*3^sin2x − 3 = 0 Δ = ... itd

tryg: 3^sin2x=t ,t>0 t²−2t−3=0 Δ=16 t=−1/sprz. t=3⇒3^sin2x=3¹ sin²x=1 /√ sinx=1 v sinx=−1

	π		π
x=		+2kπ v x=−		+2kπ
	2		2

	π
a w odpowiediach jest: x=		+kπ... mam błąd?
	2

Bogdan: Narysuj na osi liczbowej rozwiązania: sinx = 1 oraz sinx = −1:

	π		π
x =		+ k*2π lub x = −		+ k*2π.
	2		2

	π
Zobaczysz odpowiedź: x =		+ k*π, lub oznacza sumę zbiorów.
	2

tryg: 491. kolejny problem rozwiąż równanie: 4(log₂cosx)²+log₂(1+cos2x)=3 zał: cosx>0 i 1+cos2x>0

	π
x∊(−		+2kπ;{π}{2}+2kπ) cos2x+sin2x+cos2x−sin2x>0
	2

2cos²x>0 cosx≠0

	π
x≠		+kπ
	2

dobrze? rozw: 4log²₂(cos²x)+log₂(2cos²x)−3=0 log²₂(cos²x)⁴+log₂2+log₂cos²x−3=0 log²₂(cos²x)⁴+log₂cos²x−2=0 log₂cos²x=t t²+t−2=0 Δ=1+8=9 t=−2⇒log₂cos²x=−2⇒0,25=cos²x /√

	1		1
cosx=		v cosx=−
	2		2

	π		π		2		5
x=		+2kπ v x=−		+2kπ x=		π+2kπ v x=		π+2kπ
	3		3		3		3

t=1⇒log₂cos²x=1⇒cos²x=2⇒cosx=√2/sprz. v cosx=−√2/sprz.

	π		π
w odpowiedziach podali x=		+2kπ v x=−		+2kπ czy to oznacza, że dwa pozostałe
	3		3

rozwiązania wypadają z dziedziny czy się dublują?

tryg: ponawiam pytanie, bo sama sobie nie odpowiedziałam...

tryg: do tego pytania pojawiło się kolejne z innym zadaniem. proszę o odpowiedź na oba. rozwiąż równanie: (¹₂)^log2_0,5sinx+(sinx)^log_0,5sinx=1 zrobiłam założenia: sinx>0 i sinx≠1

	π
x∊(2kπ;π+2kπ)−{		+2kπ} k∊ℂ
	2

zaczęłam tak:

	π
(sin		)log20,5sinx+(sinx)log0,5sinx=1
	6

ale nie wiem co dalej...

tryg: ponawiam...

tryg: proszę o podpowiedź, wyjaśnienia

tryg: proszę o podpowiedź, wyjaśnienia

Bogdan: Podpowiedzi: 4log²_ab ≠ log_ab⁴ log_a(2b) = log_a2 + log_ab

tryg: Bogdanie, do czego są te podpowiedzi? do ostaniego zadania, z którym nie wiem co dalej, czy do wcześniejszego pytania? bo tak mi się zdaje że do wcześniejszego to bardziej pasuje, ale nic z tego nie zrozumiałam...

tryg:

xyz: Witam, mam do rozwiązania następujące zadanie : 2x² − 2(2cosα − 1)x + 2cos²α − 5cosα + 2= 0 i pytanie: dla jakich wartości ma 2 rozwiązania?

Godzio: Żeby były 2 rozwiązania to delta musi być większa lub równa zero: Δ ≥ 0 Δ = 4(4cos²α − 4cosα + 1) − 8(2cos²α − 5cosα + 2) = 16cos²α − 16cosα + 4 − 16cos²α + 40cosα − 16 = 24cosα − 12 ≥ 0 /:12 2cosα − 1 ≥ 0

	1
cosα ≥
	2

A to już prosta nierówność do rozwiązania

Ernest: 2⁽5−cos2x)−36*2^sin⁽2x)+ 2³=0