Proszę o pomoc...
magdalena.: Błagam pomóżcie mi w tym zadaniu

Wał ochronny ma przekrój w kształcie trapezu
równoramiennego, przy czym górna szerokość wału wynosi 5 m, natomiast boczne nasypy o długości
6 m są nachylone do poziomu pod kątem 60 stopni. Oblicz dolną szerokość wału. Ile m
3 ziemi
potrzeba do usypania takiego wału o długości 1 km?
12 gru 00:14
kaz:
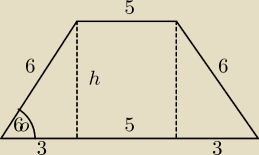
12 gru 12:06
R.W.16l:
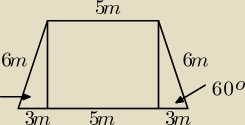
szerokość dolnego wału = 5m + 6m=11m
V=Pp*H
h=1000m
| | 16m*2√3m | | 32√3m2 | |
Pp= |
| = |
| =16√3m2 |
| | 2 | | 2 | |
V= 16000
√3m
3
dobrze?
12 gru 12:11
R.W.16l: ja to robiłem na zasadzie złotego trójkąta 30:60:90 stopni,....
ale fakt, pomyliłem się

h = 3
√3
Pp=24
√3m
2
V=24000
√3m
3
i tak inaczej...
12 gru 12:13
kaz: pominąłem h we wzorze na pole trapezu
| | a+b | |
V= |
| h=8*3√3*1000=24000√3m3 |
| | 2 | |
12 gru 12:19
Godzio:
H=1km=1000m
V=Pp*H= 24
√3*1000=24000
√3 = 41520 m
3
kaz, nieywzglęniła h w podstawie
12 gru 12:27
Godzio: przy zadaniach tego typu ( "rzeczywistych" ) należy podawać zawsze odpowiedź przybliżoną
12 gru 12:27
kaz: kaz to on
12 gru 12:30
Godzio: sorki

12 gru 12:33
R.W.16l: będę pamiętał

c do przybliżenia
12 gru 14:27
 Wał ochronny ma przekrój w kształcie trapezu
równoramiennego, przy czym górna szerokość wału wynosi 5 m, natomiast boczne nasypy o długości
6 m są nachylone do poziomu pod kątem 60 stopni. Oblicz dolną szerokość wału. Ile m3 ziemi
potrzeba do usypania takiego wału o długości 1 km?
Wał ochronny ma przekrój w kształcie trapezu
równoramiennego, przy czym górna szerokość wału wynosi 5 m, natomiast boczne nasypy o długości
6 m są nachylone do poziomu pod kątem 60 stopni. Oblicz dolną szerokość wału. Ile m3 ziemi
potrzeba do usypania takiego wału o długości 1 km?


 h = 3√3
Pp=24√3m2
V=24000√3m3
i tak inaczej...
h = 3√3
Pp=24√3m2
V=24000√3m3
i tak inaczej...


 c do przybliżenia
c do przybliżenia