 Witam, przygotowuję się do sprawdzianu z geometrii analitycznej i utknęłam przy tym zadaniu.
Wiem, że na tej stronie zostało już rozwiązane (https://matematykaszkolna.pl/forum/262368.html) ale na pewno jest kilka sposobów, a
tamtego nie łapię.
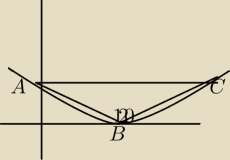
Dwa wierzchołki trójkąta równoramiennego ABC znajdują się na paraboli o równaniu
y=14(x−4)2, zaś trzecim wierzchołkiem trójkąta jest wierzchołek paraboli. Wyznacz
współrzędne wierzchołków tego trójkąta, jeśli wiadomo, że kąt rozwarty tego trójkąta ma miarę
120 st.
Witam, przygotowuję się do sprawdzianu z geometrii analitycznej i utknęłam przy tym zadaniu.
Wiem, że na tej stronie zostało już rozwiązane (https://matematykaszkolna.pl/forum/262368.html) ale na pewno jest kilka sposobów, a
tamtego nie łapię.
Dwa wierzchołki trójkąta równoramiennego ABC znajdują się na paraboli o równaniu
y=14(x−4)2, zaś trzecim wierzchołkiem trójkąta jest wierzchołek paraboli. Wyznacz
współrzędne wierzchołków tego trójkąta, jeśli wiadomo, że kąt rozwarty tego trójkąta ma miarę
120 st.
| √3 | ||
Doszłam do tego, że a prostej BC wynosi | , bo jest równy tg30 st. | |
| 3 |


