Funkcja wymierna
Shifti:
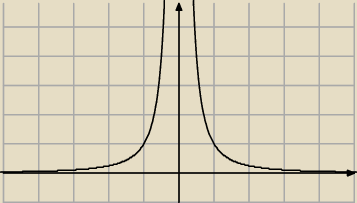
| | 1 | |
Punkty P i Q o tej samej rzędnej należą do wykresu funkcji f(x)= |
| . (rysunek) Punkt R |
| | x2 | |
należy do prostej y = −4. Wykaż, że pole trójkąta PQR jest większe lub równe 4.
Zapisuję P i Q przy użyciu f(x)
IPQI = 2x
jeszcze muszę wyliczyć h do pola, jakaś wskazówka ?
11 lis 10:24
sushi_gg6397228:
dorysuj prostą y= −4 zaznacz gdzieś punkt na prostej
na wykresie zaznacz gdzies P i Q
narysuj poglądowy trójkąt
11 lis 10:29
Shifti:
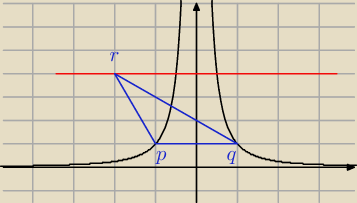
11 lis 10:42
Shifti:
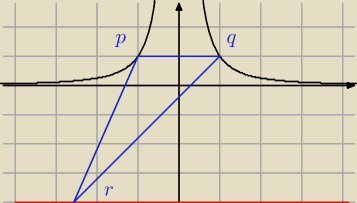
teraz dobrze

11 lis 10:44
sushi_gg6397228:
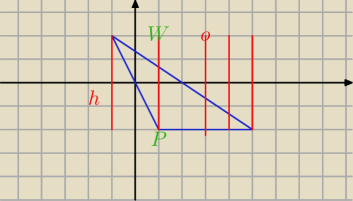
odcinki czerwone są tej samej długości
współrzędne W (x; −4)
h=|WP|= ....
11 lis 10:46
marek: w rozwiązaniu zadania jest założenie, że x>0, może ktoś powiedzieć skąd to założenie?
28 lut 16:34
marek: czy to po prostu żeby P i Q nie zamieniło się miejscami
28 lut 22:57
Nela: Wysokość trójkąta to
h=(1/x2)−(−4)
natomiast podstawa to
a=2x
zatem jego pole to
P=[(1/x2)+4]*(1/2)*2x=[4(x2)+1]/x
robimy z tego funkcję dla x>0
f(x)=[4(x2)+1]/x
i szukamy jej minimalnej wartości
d/dx=(4(x2)−1)/(x2)
miejsca zerowe pochodnej to x=1/2 i x=−1/2, ale to drugie nie należy do dziedziny
sta najmniejsze pole trójkąta zgodnego z założeniami zadania jest dla x=1/2
i wynosi 4
c.n.d.
27 maj 12:05


 teraz dobrze
teraz dobrze 
 odcinki czerwone są tej samej długości
współrzędne W (x; −4)
odcinki czerwone są tej samej długości
współrzędne W (x; −4)