wartość najmniejsza onaa: f(x)=cos²x−sinx znjadz wartość najmniejszą i największa zrobiłam to tak: f(x)=sin²x−sinx−1 sinx=t f(x)=t²−t−1 Δ=5 wartość najmniejsza w wierzchołku bo ramiona skierowane do góry q=−5/4 a jak obliczyć wartość największa będę wdzięczna za wszelką pomoc.... z góry dziękuje

Godzio:

	1
p=
	2

postać kanoniczna:

	1		5
f(x) = (sinx−		)−
	2		4

	1		5
z tego wynika że wykres sin jesej przesunięty o wektro v[		, −		]
	2		4

poradzisz sobie dalej ?

Godzio:

	1
p=
	2

postać kanoniczna:

	1		5
f(x) = (sinx−		)−
	2		4

	1		5
z tego wynika że wykres sin jesej przesunięty o wektro v[		, −		]
	2		4

poradzisz sobie dalej ?

onaa: tak dzieki

onaa: nie poradze jednak:( wart. najwieksza wychodzi mi ze to jest −1/2 a najmniejsza −2,25 dobrze

Godzio:

	1
ta		na nie interesuje bo to prawo/lewo
	2

patrzymy na q

	5		1
q=−		=> wykres jest obnizony o 1		w dół max początkowe było w 1
	4		4

	1		1
1−1		=−
	4		4

minimum było w −1

	1
−1−1		=−2,25
	4

AS: Błąd w pierwszym wierszu f(x) = 1 − sin^x − sinx

onaa: f(x)=−sin²x−sinx+1 sinx=t f(x)=−t²−t+1 Δ=5

onaa:

	1
p=−
	2

	5
q=
	2

	5
min −1−		=−3,5
	2

	5
max 1−		=1,5
	2

teraz jest ok?

Godzio: cos²x=1−sinx² więc f(x) = sin²x − sinx +1 Δ=1−4 = −3

	3
q=
	4

	3
max : 1
	4

	1
min : −
	4

onaa:

	1
p=−
	2

	5
q=
	4

	5
min −1−		=−2,25
	4

	5
max 1−		=−0,25
	4

teraz jest ok?

onaa: a w odpowiedziach jest −1 i 1,25:(

onaa: f(x) = sin²x − sinx +1 zapomniałeś minusa... f(x) = −sin²x − sinx +1

onaa: f(x) = sin²x − sinx +1 zapomniałeś minusa... f(x) = −sin²x − sinx +1

Godzio: albo źle przykład przepisałaś, moim zdaniem ta odpowiedź nie jest możliwa

Godzio: sprawdź czy dobrze przepisałaś .

onaa: dobrze przepisałam no i lipa:( jak nie dasz rade rozwiązać to już trudno, może sama do tego jakoś dojdę...

Godzio: ale masz przykład tak : f(x) = cos²x − sinx czy tak: f(x) = −cos²x − sinx

onaa: tak:cos²−sinx

onaa: cos²x−sinx

Godzio: już chyba wiem w czym rzecz czekaj moment

onaa: ok

Godzio: zjadłem minusa, a ty plusa f(x)=−sin²x − sinx +1 Δ=1+4=5

	−5		5
q=		=
	−4		4

czyli tak jak mówiłaś max jest w wierzcholku a minimum 1 bo sinx może wynosić <−1,1> więc a jeśli podstawi się pod sinx 1 lub −1 to powstanie 1

Godzio: zapomniałem kompletnie że w postaci kanonicznej jest kwadrat i przesuwa się funkcja sin²x a nie sinx

kolo: dziękuję ślicznie dozgonna wdzięczność!

Godzio: naczy nie miało być tak: skoro sinx nalezy do <−1,1> to najmniejsza wartość jest w −1

onaa: a największa w wierzchołku ok

Godzio: sprawdź jeszcze raz odpowiedź bo coś mi nie pasi

onaa: m=−1, M=1,25

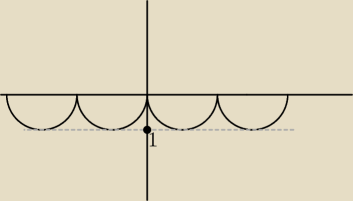
Godzio: wydaje mi się jednak że to jest nie możliwe to co narysowalem wykres f(x) = −sin²x więc jeśli obliczyliśmy q=1,25 to jeśli to przesuniemy do góry o tyle to otrzymujemy max 1,25 i min 0,25

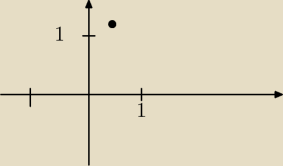
onaa: wartość max w wierzchołku: 5/4 wartość min: −1 bo funkcja należy do przedziału<−1;1> a ramiona ma skierowane do dołu