Cosinus miedzy scianami bocznymi ostroslupa
Szymeg: Podstawą ostrosłupa jest prostokąt o bokach 4 i 4√2 . Wszystkie krawędzie boczne ostrosłupa
mają długość 4. Oblicz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego
ostrosłupa.
I tu zaczyna sie problem.
Znalazlem identyczne zadanie w dwoch ksiazkach. W jednej wynik wynosi −√21/21 a w drugiej
−√3/3
Zadanie licze z porownan pol trojkatow, a na koncu z tw. cosinusow. Ktory wynik jest poprawny?
9 lis 23:59
Godzio:
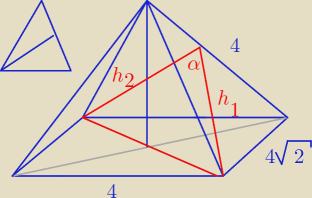
Wysokość trójkąta równoramiennego opuszczona na podstawęL h
(2
√2)
2 + h
2 = 4
2
h = 2
√2
Wysokość będąca ramieniem czerwonego trójkąta: h
1
h
1 = 4
Wysokość trójkąta równobocznego będącego drugą ścianą boczną: h
2
Przekątna podstawy
d
2 = (4
√2)
2 + 4
2
d
2 = 32 + 16
d
2 = 48
d = 4
√3
Twierdzenie cosinusów
d
2 = h
12 + h
22 − 2h
1h
2cosα
48 = 16 + 12 − 16
√3cosα
20 = − 16
√3cosα
| | 5 | | 5√3 | |
cosα = − |
| = − |
| |
| | 4√3 | | 12 | |
10 lis 00:06
Szymeg: Wychodzi mi dokladnie to samo, jednak odpowiedz jest inna, moze po prostu wysokosci scian
bkcznych sa na roznych wysokosciach?
10 lis 00:08
Godzio:
Hmmm
10 lis 00:11
Godzio:
Chyba masz rację, zaraz pomyślę.
10 lis 00:12
Szymeg: Jesli sie spotykaja w polowie 4, to wychodzi ta pierwsza odpowiedz
jednak w ksiazce CKE wychodzi ta druga odpowiedz
10 lis 00:17
Godzio:
Już widzę błąd w rozumowaniu u siebie, trójkąt 4,4,4√2 jest prostokątny, więc bez sensu
poprowadzona u mnie wysokość, mam już pomysł, postaram się zaraz napisać rozwiązanie. Spotkają
się w połowie.
10 lis 00:20
Godzio:
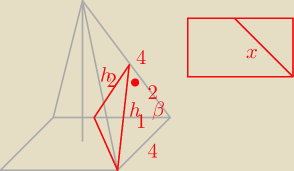
β = 45
o ⇒ h
2 = 2
h
1 = 2
√3
x
2 = (2
√2)
2 + 4
2 = 8 + 16 = 24
x = 2
√6
Z tw. cosinusów:
24 = 12 + 4 − 8
√3cosα
8 = −8
√3cosα
10 lis 00:24
Szymeg: Wow, dzieki stary, meczylem sie z tym dobre dwie godzinki
10 lis 00:33
Godzio:
Wszystko jasne? Bo trochę skrótowo to zapisałem ..
10 lis 00:34
Szymeg: Nie wiem tylko dlaczego jedna z wysokosci to 2
10 lis 00:38
Godzio:
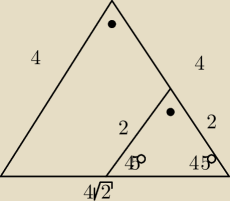
Prowadząc tą 'wysokość' otrzymujemy trójkąt równoramienny, ponieważ wysokość z trójkąta
równobocznego poszła do środka, to ta też musiała, 4/2 = 2 stąd mamy bok tego trójkąta, który
jest jednocześnie naszą 'wysokością'
10 lis 00:44
Szymeg: Aaaa.. bardzo pomyslowe, nie wiem jak na to wpadles, ale dziala, jeszcze raz wielkie dzieki
10 lis 00:51