 Zaznacz zbiór na płaszczyźnie zespolonej
A = { z ∊ C: |z + i| > re(z) + 1
z = a + bi
|a + i(b+1)| > a + 1
√a2 + b2 + 2b + 1 > a + 1
a2 + b2 +2b + 1 > a2 + 2a + 1
b2 +2b > 2a
i teraz nie wiem jak dalej to dkończyć?
Pomożecie
Zaznacz zbiór na płaszczyźnie zespolonej
A = { z ∊ C: |z + i| > re(z) + 1
z = a + bi
|a + i(b+1)| > a + 1
√a2 + b2 + 2b + 1 > a + 1
a2 + b2 +2b + 1 > a2 + 2a + 1
b2 +2b > 2a
i teraz nie wiem jak dalej to dkończyć?
Pomożecie 
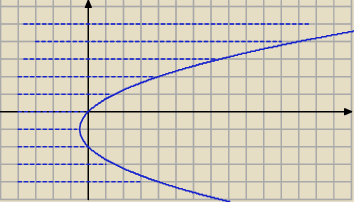 (b+1)2>2a+1
|b+1|>√2a+1
(b+1)2>2a+1
|b+1|>√2a+1

 Przy oznaczeniu
z=x+i*y
otrzymujesz :
|z+i|=√x+(y+1)2
√x2+(y+1)2>x+1 /2
x2+(y+1)2>x2+2x+1⇔(y+1)2>2x+1
rysujemy krzywą:
(y+1)2=2x+1
stąd :
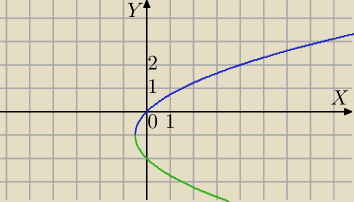
y+1=√2x+1 dla x≥−1 ⇔
y=√2x+1−1
lub
y=−√2x+1−1
Teraz wybierasz obszar.
Można to zrobić inaczej , narysować parabolę o poziomej osi symetrii>
Przy oznaczeniu
z=x+i*y
otrzymujesz :
|z+i|=√x+(y+1)2
√x2+(y+1)2>x+1 /2
x2+(y+1)2>x2+2x+1⇔(y+1)2>2x+1
rysujemy krzywą:
(y+1)2=2x+1
stąd :
y+1=√2x+1 dla x≥−1 ⇔
y=√2x+1−1
lub
y=−√2x+1−1
Teraz wybierasz obszar.
Można to zrobić inaczej , narysować parabolę o poziomej osi symetrii>
| 1 | ||
x= | y2+y | |
| 2 |
| −1 | ||
yw= | =−1 | |
| 1 |
| 1 | 1 | |||
xw= | −1=− | |||
| 2 | 2 |
| 1 | ||
W=(− | , −1) | |
| 2 |