Argument główny liczby zespolonej Patryk: Liczby zespolone − argument główny. Wytłumaczy mi ktoś dlaczego Arg(z+i) przedstawiony graficznie ma punkt w (0, −i)? Wiem, że dla Arg(z) jest to punkt (0,0) Czyli chodzi tutaj o to, że musi być takie przesunięcie punktu, po którym wyjdzie punkt (0, 0)? Czyli nasz punkt (0, −i) jak przesuniemy o +i wzdłuż osi IM da nam (0, 0), tak?

J: czy wiesz, co to jest argument liczby zespolonej ?

Patryk: Kąt pomiędzy osią Re oraz prostą łączącą początek układu z punktem Z, takim, że jest nie większy od 180 stopni, tak?

Patryk: Tzn w tym przedziale to główny

J: jest to kąt z przedziału [0,2π) , a skoro tak , to jak może to być punkt ?

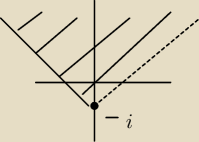
Patryk: Chodzi mi konkretniej o taki przykład:

π		3π
	< Arg(z+i) ≤
4		4

I moje pytanie brzmi, dlaczego akurat z tego punktu jest liczony argument liczby zespolonej?

Patryk: Źle sformułowałem pytanie, przepraszam. Chodziło mi o punkt zaznaczony powyżej

J: a.. to zmienia postać rzeczy ... jest to zbiór wszystkich liczb zespolonych: w = z − ( −1), których argument jest zawarty w podanym przedziale.. graficznie przesuwamy wierzchołek tego kąta z punktu (0,0) o wektor : z₀ = − i

Patryk: A dlaczego o −i, a nie +i? Mógłby Pan/Pani podać jakiś przykład na dwóch współrzędnych?

J: (z + i) = [z − (−i)]

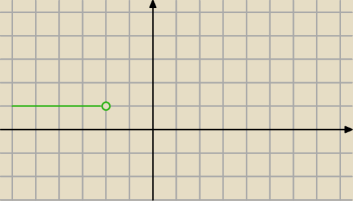
J: Arg ( z + 2 − 1) = π ⇔ Arg [ z − ( −2 + 1) ] = π ( liczby zaznaczone na zielono )

J: zamias 1 miało być oczywiście "i" Arg ( z + 2 − i) = π ⇔ Arg [z − ( −2 + i) ] = π

Patryk: Wszystko jasne Dziękuję serdecznie za pomoc! Pozdrawiam