Twa Tra: Przy zadaniach z parametrem i funkcja liniowa mam pytania dla jakiego m rozwiązaniem równania jest para liczb o przeciwnych znakach. Równanie ma postać |z−1|=m−2. Mógłby mi ktoś na rysunku przedstawić kiedy będą jakie opcje ? Kiedy równanie będzie miało rozwiązanie jako parę liczb o tych samych znakach itp. ?

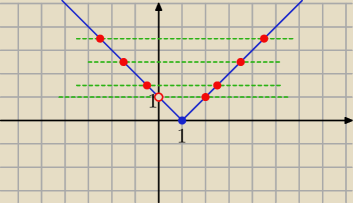
Eta: f(x)=|x−1| g(x)=m−2 f(x)=g(x) równanie ma pierwiastki różnych znaków ( jeden po lewej drugi po prawej stronie dla m−2>1 ⇒ m........

Tra: Odp ma wyjść m∊(−1;∞)

Eta: Pewnie w zapisie jest m+2 a Ty podajesz m−2

Tra: Ale dla równania |x−1|=m+2 . Pomyliłem się. Czy mogę to siebie rozpisać z definicji modułu na 1) x−3=m 2) −x−1=m Narysować obie proste i co w tedy mam wziąć pod uwagę ? A kiedy rozwiązaniem byłaby para liczb dodatnich/tych samych znakow itp. ?

Tra: Tak tak, pisze z telefonu, pisałem równanie z pamięci. Przepraszam.

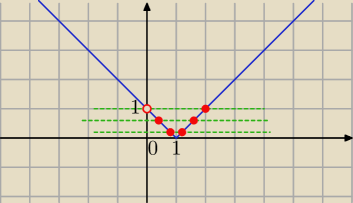
Eta: 1/ m+2>1 ⇒ m>−1 ⇒ m∊( −1, ∞) i teraz zgadza się 2/ para rozwiązań dodatnich wtedy gdy 0<m+2<1 ⇔ m+2<1 i m+2>0 ⇔ m∊(−2,−1)

Eta:

Tra: Dziękuję. A jak bym narysował 1) pr. X−3 oraz pr. −x−1 to gdzie były by rozwiązania?