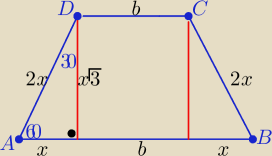
Trapez Hello: Pole trapezu rownoramiennego o kącie przy podstawie 60° jest równe 2√3. Wyznacz wymiary trapezu o najmniejszym obwodzie. Uzasadnij, że trapez ten można wpisać w okrąg i oblicz promień tego okręgu. Proszę o jakąkolwiek inspiracje, bo nie mam już pomysłu jak to ruszyć.

Eta: P=2√3 x>0

	2−x2
P= (x+b)*x√3 ⇒ x(x+b)=2 ⇒ b=
	x

	4x2+4
L=4x+2b to L(x)=
	x

	4x2−4
L'(x)=
	x2

	2−1
L(x)=0 ⇔ x2=1 ⇒ x=1 to b=		=1 ⇒ b=x i h=√3 , |AB|=3x=3
	1

|BC|=|AD|=2x=2 warunek wpisania okręgu w trapez : |AB|+|CD|= |AD|+|BC| ⇒ 4=4 −− zachodzi w ten trapez można wpisać okrąg

	3+1
Sprawdzam pole : P=		*√3= 2√3 ( ok)
	2

Eta: Jeszcze :

	√3
2r=h ⇒ r=
	2

Eta: Poprawiam zapis: L^'(x)=0 ⇔ ...

Eta: Dostał nie tylko .."inspiracje" i ma w .......................