w rombie dany jest kąt ostry o mierze 60 i krótsza przekątna o długości 4cm obli agnieszka: w rombie dany jest kąt ostry o mierze 60 i krótsza przekątna o długości 4cm oblicz pole i obwód tego rombu

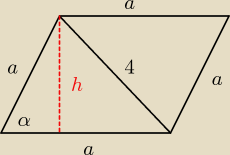
Nikka: Z tw. cosinusów obliczasz długość boku a: 4² = a²+a² − 2*a*a*cos60^o

	1
16 = 2a2 − 2a2*
	2

a² = 16 cm² a = 4 cm Obw = 4a = 4* 4 cm = 16 cm

	h
sinα =
	a

	h
sin60o =
	4cm

√3		h
	=		→ h = 2√3cm
2		4cm

P=a*h P = 4cm*2√3cm = 8√3 cm²

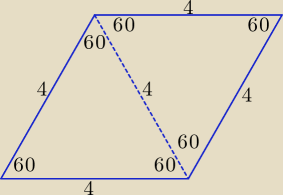Bogdan: Jeśli miara kąta ostrego rombu jest równa 60^o, to miara kąta rozwartego jest równa 120^o. Przekątne rombu są dwusiecznymi kątów wewnętrznych. Krótsza przekątna rombu w takim rombie dzieli go na 2 trójkąty równoboczne. Stąd długość boku jest równa długości krótszej przekątnej. a = 4, obwód L = 4a = 16,

	√3
pole rombu P = a2*sinα ⇒ P = 42*sin60o = 16*		= 8√3
	2

Warto poszukiwać najprostszych, a przez to zajmujących mniej czasu i łatwiejszych rachunkowo rozwiązań.