zbiór wartości
Dziwny człek: wyznacz zbiór wartości funkcji f
| | 1 | | π | | 5π | |
f(x)= |
| x∊< |
| , |
| > |
| | sinx | | 4 | | 6 | |
8 lis 16:21
sushi_gg6397228:
jakiś własny wkład w to zadanie ?
8 lis 17:30
freeszpak: patrzysz jakie wartości przyjmują funkcje z mianowników (oczywiście wartości mają być różne od
zera) a następnie się zastanów jak to, że bierzemy odwrotność tych wartości na nie wpływa i to
będzie odpowiedź

8 lis 17:31
Dziwny człek: to znaczy

x
2−4x+3≠0
Δ=4
x
1=4+2/2=3
x
2=4−2/2=1
f(4)=(x−3)(x−1)=1*3=3
f(6)=(6−3)(6−1)=15
| | 1 | | 1 | |
odwrotność czyli |
| i |
| |
| | 15 | | 3 | |
dobrze

8 lis 17:46
sushi_gg6397228:
a policzyłeś "p" i sprawdziłeś
8 lis 17:49
Dziwny człek: sinx∊<−1,1>
i tutaj nie wiem za bardzo?
8 lis 17:49
Dziwny człek: f(x
w)=f(2)=4−8+3=−1
8 lis 17:51
sushi_gg6397228:
czy p ∊ <4;6>

rób jedno zadanie, a nie wrzucasz już drugie i sie zaraz popitoli
8 lis 17:54
Dziwny człek: Podstawić pod to
| | √2 | | 1 | |
f( |
| )= |
| =2√2/2=√2 |
| | 2 | | √2{2} | |
8 lis 17:57
Dziwny człek: nie p nie należy od <4,6> gdyby należało to nie sprawdzalibyśmy na krańcach przedziałów.Słuszna
uwaga dzieki
8 lis 17:58
8 lis 17:59
sushi_gg6397228:
jak policzymy "p" , to też sprawdzamy na krańcach−−> bo trzeba znaleźć drugą wartość
odpowiedz do przykładu a) ...
8 lis 18:00
8 lis 18:03
sushi_gg6397228:
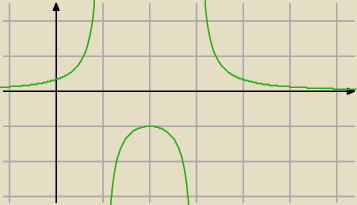
podałeś odpowiedź składającą się tylko z dwóch punktów −−> do bani
8 lis 18:07
Dziwny człek: aha już rozumiem to
dzięki za wykres.
8 lis 18:10
sushi_gg6397228:
jest OK
2) rysujesz wykres sinusa i zaznaczasz podany zakres
8 lis 18:12
misiak:
b)
| | π | | √2 | | 5π | | 1 | |
sin( |
| )= |
| i sin( |
| )= |
| |
| | 4 | | 2 | | 6 | | 2 | |
| π | | 5π | | 1 | |
| ≤ x ≤ |
| ⇒ |
| ≤ sinx ≤ 1 |
| 4 | | 6 | | 2 | |
8 lis 18:12
Dziwny człek: jakim cudem powstało to przekształcenie w linijce 3? misiak?
8 lis 18:15
misiak:
widać to na wykresie funkcji sinus
8 lis 18:17
misiak:
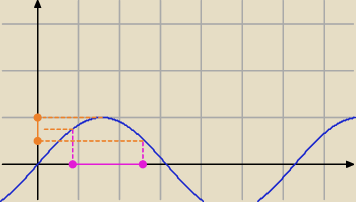
8 lis 18:20
Dziwny człek: dzięki już to widze. Wiedziałem jak to wygląda ale myślałem że trzeba część wspólną wyznaczyć.

dla was <3 dzieki
8 lis 18:22

 x2−4x+3≠0
Δ=4
x1=4+2/2=3
x2=4−2/2=1
f(4)=(x−3)(x−1)=1*3=3
f(6)=(6−3)(6−1)=15
x2−4x+3≠0
Δ=4
x1=4+2/2=3
x2=4−2/2=1
f(4)=(x−3)(x−1)=1*3=3
f(6)=(6−3)(6−1)=15

 rób jedno zadanie, a nie wrzucasz już drugie i sie zaraz popitoli
rób jedno zadanie, a nie wrzucasz już drugie i sie zaraz popitoli
 podałeś odpowiedź składającą się tylko z dwóch punktów −−> do bani
podałeś odpowiedź składającą się tylko z dwóch punktów −−> do bani

 dla was <3 dzieki
dla was <3 dzieki