planimetria olphA: określ, który z trójkątów prostokątnych wpisanych w okrąg o promieniu r ma najwieksze pole

Tadeusz: podstawa tego trójkąta to ... średnica okręgu P_max ...dla h=r

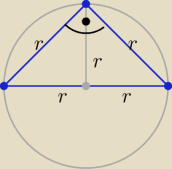
Eta: P_max ma trójkąt prostokątny równoramienny o ramionach długości r

olphA: a udowodnić to jakoś z pochodnej?

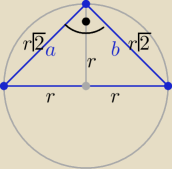
Eta: Poprawiam oznaczenia na rys. (przez nieuwagę źle oznaczyłam) ma być : trójkąt równoramienny o ramionach długości r√2 a, b>0

	1
P=		ab i a2+b2=4r2 ⇒ a=√4r2−b2
	2

	1
P(b)=		*√4r2−b2*b
	2

	1		−2b		1		4r2−b2−b2
P'(b)=		( √4r2−b2+b*		=		(
	2		2√4r2−b2		2		√4r2−b2

P^'(b)=0 ⇔ 4r²−2b²=0 ⇔ b= √2*r to a= √4r²−r²= √2r²= √2*r Dla a=b=r√2 trójkąt prostokątny wpisany w okrąg o promieniu r ma największe pole