Zbadaj liczbe rozwiazan Stokrotka: Pomocy :c zbadaj liczbę rozwiązań równania w zależności od wartości parametru m (m należy R) 1) 4 * 2^|x−1| = m

Aga1.: Narysuj wykres funkcji y=4*2^Ix−1I oraz proste y=m dla różnych m i patrz ile punktów wspólnych ma prosta z wykresem

Stokrotka: Jak narysowac ten wykres bo w tym mam problem ?

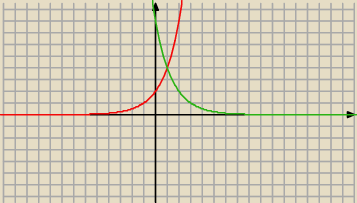
5-latek: dla x≥1 równanie ma postac 4*2^x−1=m a dla x<1 ma postac 4*2^1−x=m

Stokrotka: Dzieki

Misiek: Wytlumaczy ktos jak to po kolei narysowac?

Misiek: Bo ten wyres jest zle narysowany ...

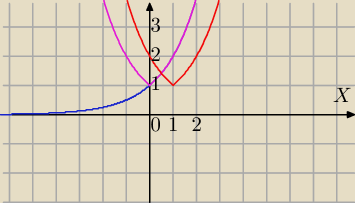
Mila: 4 * 2^|x−1| = m /:4

	m
2|x−1|=
	4

Rysujemy wykres f(x)=2^|x−1|: 1) y=2^x symetria względem OY tej części wykresu z prawej strony OY ( tę z lewej pomijamy, to co zostało niebieskie)⇒ 2) y=2^|x| ⇒T_[1,0]⇒ 3) f(x)=2^|x−1| Jeśli nie jesteś pewny to sprawdź kilka charakterystycznych punktów. f(1)=2^|1−1|=2⁰=1 f(0)=2^|0−1|=2¹=2 f(2)=2^|2−1|=2

5-latek: A dlaczego twierdzisz z eten wykres co narysowałem jest zly ? ja jestem jeszcze stara szkola i tam gdzie nie ma takiej potrzeby nie bawie się w przekształcenia jeśli mam narysować wykres np. y=x²+5 to nie będę się bawil tak robie tabelke y=x² i potem go przesuwam o wektor [0,5] bo to by było bez sensu Tak samo tutaj wezmy dla x≥1 dla x=1 y= 4*2¹⁻¹=4 (tak jest na wykresie ? dla x=2 y=4*2²⁻¹= 4*2=8 jest tak ? Weź teraz w druga strone x=0 to y= 4*2¹⁻⁰= 8 jest tak ?

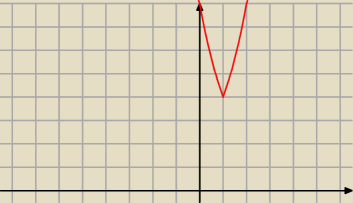
Aga1.: @5−latek docelowy wykres funkcji y=2²*2^|x−1|=2^|x−1|+2 wygląda tak . Widocznie ten ktoś nie umiał skorzystać z Twojej wskazówki.