2 zadania maturalne heaVen: 1.samochód przejechał 180 jadąc se stałą prędkością. gdyby jechał o 30km/h szybciej to czas przejazdy zmniejszyłby się o 1h. oblicz z jaką prędkością jechał samochód. 2. punkty A=(−2;4) B=(−2;−2) C=(5;−3) D=(1;4) są wierzchołkami czworokąta oblicz punkt przecięcia przekątnych BARDZO DZIĘKUJĘ ZA POMOC!

AROB: pomogę

AROB: Zad. 1. I sytuacja II sytuacja −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− prędkość V V + 30 droga 180 180 czas t t − 1 S = const. S = V * t Otrzymujemy układ równań: V * t = 180 (V+30)(t − 1) = 180

	180
V =
	t

	180
(		+ 30)(t − 1) = 180
	t

	180
180 −		+ 30t − 30 = 180
	t

	180
150 −		+ 30t = 180 /*t
	t

150t − 180 + 30t² = 180t 30t² − 30t − 180 = 0 /:30 t² − t − 6 = 0 Δ = 25, √Δ = 5, t₁=3, t₂ = −2 (sprzeczne z treścią)

	180
Czyli t=3, więc V =		= 60 [km/h]
	3

Zaraz poślę zad. 2.

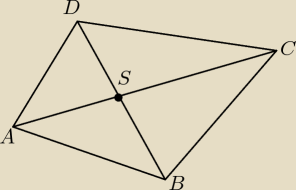
AROB: A(−2,4), B(−2,−2), C(5,3), D(1,4) S=? Wyznaczamy równania prostych zawierające przekątne czworokąta. Prosta AC: (y − y_A)(x_B−x_A) = (x−x_A)(y_B−y_A) (y−4)(−2+2) = (x+2)(−2−4) 0 = −6(x+2) ⇒ 6x = −12 ⇒ x = −2

	yD−yB
Prosta BD: y−yB =		(x−xB)
	xD−xB

	4+2
y+2 =		(x+2)
	1+2

y = 2(x+2) − 2 ⇒ y = 2x+2 Współrzędne punktu S wyznacza się z układu równań: y=2x+2 x = −2 Stąd: y = 2*(−2)+2= −2 Czyli S(−2, −2).

heaVen: WIELKIE DZIĘKI

janek: ∞≥∊⊂∫←→⇒