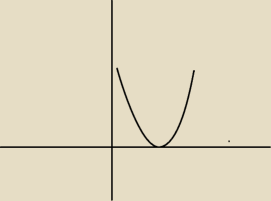
suma rozwiązań funkcji okresowej Marusia: mam funkcję okresową o T=4 i polecenie: oblicz sumę wszystkich rozwiązań równania f(0)=4 należących do przedziału <0;400>. To zadanie było już parę razy na forum, ale podpowiedzi nie przydały mi się. Nie miałam jeszcze ciągów. Ja zaczęłam tak: dla podstawowego okresu f(x)=4 dla x=0 i x=4 (mam 2rozwiązania) dla pozostałych okresów mam po jednym rozwiązaniu, więc w sumie mam 101 rozwiązań w przedziale <0;400> Podpowie ktoś jak jak dalej? Albo jak zastosować do tego zadania wzór f(x+kT)=f(x)?

Marusia: nikt nie pomoże?

Mila: T=4 f(x+k*4)=f(x) Tak jak w funkcjach trygonometrycznych: sin(x+2kπ)=sin(x)

Marusia: nie daję rady z tym zadaniem. Za x podstawiam 4 bo f(4)=4? Za k100 bo przedział<0;400>? wynik ma wyjść 20200 Z sin daję radę, bo przedziały są mniejsze i rozpisuję tak jak parę dni temu mi tłumaczyłaś wraz z PW

Marusia: Ja już doczytałam o ciągach i zastosowałam wzór na sumę początkowych wyrazów ciągu arytmetycznego i faktycznie wychodzi 20200 ale ja nie miałam jeszcze ciągów. Mila pomożesz? Ja nie muszę mieć tego na teraz. Przerabiam sobie wszystkie zadania z podręcznika i to zadanie męczy mnie już parę dni.

Eta: Możesz tak ( skoro nie miałaś ciągów) (4+8+12+.....+200) + (204+.......+392+396+400)= −−−−−−−−−−−−−− −−−−−−−−−−−−−−−−−−−− n= 50 n= 50 4+400=404 8+396=404 12+392=404 itd 200+204=404 suma jest równa 404*50= 20 200

Eta: Czy już jasne?

bezendu: Tak.

Eta: ? (jasne?

bezendu: To po prawej

Eta:

bezendu: Ale Twojej prawej (mojej lewej )

Marusia: Tak! teraz rozumiem. wczoraj nie dotrwałam do odpowiedzi. A tu rano taka niespodzianka. Bardzo dziękuję.