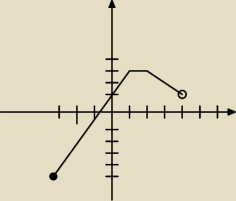
,, Ola: Pomoże ktoś mi po raz kolejny ? a)dziedzina−<−1;4) b)zbiór wartości (nie wiem jakie nawiasy) −5;3 c)wartości ekstremalne−ymax 1 ymin −5 d)miejsca zerowe x1−−1 e)przedziały monotoniczności f)argumenty,dla których funkcja przyjmuje wartości dodatnie g)argumenty,dla których funkcja przyjmuje wartości ujemne h)argumenty,dla których funkcja przyjmuje wartość 1

J: a) źle b [−5,3] c) źle d) dobrze ... popraw i pisz dalsze punkty

Ola: a)<−3;4) c)ymax 1 ymin 3 e)monotoniczna przedziałami : rosnąca −5;3 stała 1;2 malejąca 2;4

J: c) źle rosnąca − źle

Ola: to nie mam pojecia juz jak

J: jaka jest maksymalna wartość funkci , a jaka minimalna ?

Ola: c0zle napisalam ymax to 3 y min −5

Ola: wiedialam o co chodzi w c) a zle napisałam

Janek191: Teraz jest dobrze Napisałaś, że y_max = 1 , a y_min = − 5

Ola: wiem mój błąd ale już f,g,h nie wiem naprawdę

Janek191: Przedziały monotoniczności ( na osi X ), to przedziały, w których funkcja: rośnie : jest stała: maleje:

Ola: to odczytujemy tylko z osi x przedzialy monotonicznosci ?

Artur Burzynski: eee

Artur Burzyński: eee

J: tak , przedziały monotonicznośći określamy na osi OX

Ola: to co rosnąca będzie skoro odczytuje sie z x −3;1

Artur Burzyński: eeeeee nie wiem

Ola: to po co piszesz

J: tak, rosnąca dla x ∊ [−3,1]

Ola: a pomoze mi Pan teraz f,g,h

Ola: ponawiam pytanie

J: f( (−1,4) g) (−3,−1) h) x = 0

Ola: oooo jak super dziękuje bardzo Gdzie Pan się tego wszystkiego nauczył ? To jak już Pan jest to napisze Panu jeszcze jedno zadanie bo mam do niego trzy rozwiązania i nie wiem które poprawne już nie rozwiązuje więcej bo znowu mi inne wyjdzie mógłby Pan rzucić okiem i powiedzieć które jest dobre

Ola: mam takie zadanie: Rozwiąż równanie: 2(3x−7)²−(6x−4)(3x−4)=14−38x 2(9x²*2*3x*7*7x²)−(18x²−24−12x+16)=14−38x 2(9x²−42x+49)−(18x²+24−12x+16)=14−38x 18x²−84x+98−18x²+24x+12x−16=14−38x 82−48x=14−38 −48x+38=14−82 −10x=−68/:10 x=6,8 2(9x²−42x+49)−(18x²+24x−12x+16)=14−38x 18x²+84x+98−18x²4x−12x+16=14−38x 120x+114=14−38x 120x+38x=114+14 82x=128/:82 x=1⁴₆ 2(9x²−42x+49)−(18x²+24x−12x+16)=14−38x 18x²+84x+98−18x²4x−12x−16=14−38x 120x+82=14−38x 120x+38=14−82 158x=−68/:(−158) x=³⁴₇₉

5-latek: Wynik prawidłowy jest w 1 rozwiązaniu