rownanie z wartoscia bezwzgledna Svq: nie potrafilam zrobic takiego rownania : Ix + 2I + 3x =1

:): |x+2|+3x=1 czyli |x+2|=1−3x

	1
z definicji |x+2|≥0 więc 1−3x≥0 więc 1≥3x więc x≤
	3

	1
1 przypadek. x∊[−2,		]. Wtedy x+2≥0
	3

więc x+2+3x=1 czyli 4x=−1 więc x=−1/4 2. przypadek x<−2 wtedy |x+2|=−(x+2) więc −x−2+3x=1 więc 2x=3 więc x=3/2 (nie nalezy do rozważanego przedziału) Odp; x=−1/4

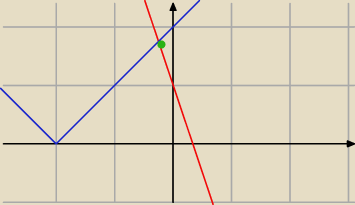
Aga1.: Lub Graficznie Ix+2I=−3x+1 y=Ix+2I niebieski y=−3x+1 czerwony Punkt wspólny zielony odp.x=−1/4

Stef: Przy rozwiązywaniu tego równania nie trzeba przenosić składnika 3x na drugą stronę

Kacper: Oczywiście, że nie trzeba, natomiast każdy ma własne pomysły.

pigor: ..., a jak nie potrafisz inaczej, to zawsze możesz niezawodnie przedziałami i np. tu tak : Ix+2I+3x=1 ⇔ (x+2<0 i −x−2+3x=1) v (x+2 ≥0 i x+2+3x=1) ⇔ ⇔ (x< −2 i 2x=3) v (x ≥ −2 i 4x= −1) ⇔ x∊∅ v x= −¹₄ ⇔ ⇔ x∊{−¹₄} . ...