Obraz i przeciwobraz 5-latek: Znajdz związki miedzy zbiorami A i f⁻¹(f(A)) Bo jak mam np. funkcje f(x)=x² i mam znaleźć f⁻¹(<0,4>) i f(<0,2>) To f⁻¹(<0,4>)= <0,2> f(<0,2>)=<0,4>

5-latek: Dlaczego A⊂f⁻¹(f(A))? Może ktoś wytlumaczyc po ludzku ?

zombi: Ale f⁻¹([0,4]) = [−2, 2], a nie samo [0, 2] Definicja przeciwobrazu mówi, że f⁻¹(B) = {x∊X : f(x)∊B} Biorąc f⁻¹({4}) = {−2, 2}. A dlaczego zawieranie takie zachodzi. Otóż weźmy funkcję chociażby taka jak f(x) = x². Zbiór f⁻¹(f(A)) wyprodukuje nam więcej iksów niż zawarte jest w A, w twoim przykładzie: A = [0, 2], f([0,2]) = [0,4], ale już f⁻¹([0,4]) = [−2, 2]. Zbiór A jest "obcięty", natomiast f⁻¹(f(A)) wybiera nam wszystkie iksy z dziedziny, więc jest nadzbiorem A.

5-latek: dzięki za odpowiedz Z tym przeciwobrazem to masz racje . Przeciez wartość funkcji y=4 jest dla x=2 i x=−2

zombi: Można to zawierania pokazać w ten sposób. Weźmiemy dowolny x ze zbioru A i pokażemy, że znajduje się również w f⁻¹(f(A)). Bierzemy dowolny x₀∊A. Teraz z definicji obrazu f(x₀)∊f(A). Teraz z definicji przeciwobrazu f⁻¹(f(A)) = {x∊X: f(x)∊f(A)}, ale przecież f(x₀)∊f(A), więc x₀∊{x∊X: f(x)∊f(A)}. Czyli x₀∊f⁻¹(f(A))

5-latek: OK Jutro się do Ciebie odezwe jeśli będę miał jeszcze jakies pytania do tego

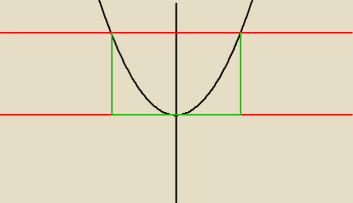
zombi: Ponadto spójrz na wykres f(x) = x², jeśli chcemy znaleźć iksy, które dają wartości od 0 do 4, to patrzymy tak: Rysujemy dwie poziome linie po igrekach, żeby zobaczyć, gdzie przecinają na wykresie nasze szukane wartości, następnie w dół rysujemy linie które wyznaczą nam ten przedział na iksach (zielona ljnia O_x)