bardzo prosze o pomoc! :
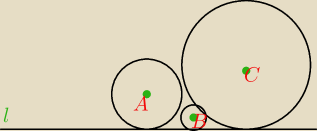
niech okregi O(A,rA), O(B,rB),O(C,rC) bedą parami styczne zewnetrzni oraz styczne do prostej
l. wykaż, że: 1/√rB = 1/√rA + 1/√rC
na rysunku nie widac, ale okregi maja byc styczne 
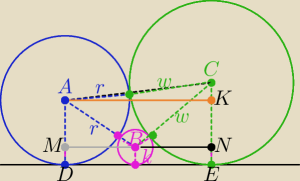Dla łatwości zapisów wprowadzam takie oznaczenia:
o(A,r) , o(B,k) , o(C,w)
(**)|AK|=|MB|+BN| i |AC|=r+w , |BC|=k+w , |AB|=r+k
z trójkątów prostokątnych : AKC i AMB i CNB
|AM|=r−k , |CN|=w−k , |CK|=w−r
z tw. Pitagorasa :
|AK|=√AC2−CK2=√((r+w)2−w−r)2= ...... = 2√rw
analogicznie : |MB|= ....= 2√rk i |BN|=...=2√kw
to z (**) √rw=√rk+√kw /2 ⇒ rw= rk+2k√rw+kw
rw= k(r+2√rw+w) ⇒ rw= k(√r+√w)2
| 1 | √r+√w | 1 | 1 | |||||
to √r*√w= √k*(√r+√w)⇒ | = | = | + | |||||
| √k | √r*√w | √w | √r |
| 1 | 1 | 1 | ||||
= | + | |||||
| √rB | √rA | √rC |
| 1 | 1 | 1 | ||||
= | + | |||||
| √k | √w | √r |
?
