.
trele: (prawo równoległoboku) wykaż, że jesli czworokat ABCD jest równoległobokiemto
2|AB|2+2|BC|2=|AC|2+|BD|2
4 lis 10:05
trele: 
4 lis 18:37
Mila:
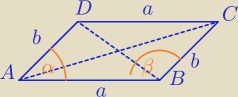
α−kąt ostry
β=180−α
cosβ=cos(180−α)=−cosα
W ΔDAB z tw. cosinusów:
|BD|
2=a
2+b
2−2*a*b*cosα
W Δ ACB:
|AC|
2=a
2+b
2−2*a*b*cosβ⇔
|AC|
2=a
2+b
2+2*a*b*cosα
|BD|
2+|AC|
2=a
2+b
2−2*a*b*cosα+a
2+b
2+2*a*b*cosα⇔
|BD|
2+|AC|
2=2a
2+2b
2⇔
|BD|
2+|AC|
2=2|AB|
2+2|BC|
2
cnw
======================
4 lis 18:47
4 lis 18:55
trele: teraz jak na to patrze to jest to takie łatwe!

jeszcze raz dziękuje

4 lis 18:56
Mila:

4 lis 19:03

 α−kąt ostry
β=180−α
cosβ=cos(180−α)=−cosα
W ΔDAB z tw. cosinusów:
|BD|2=a2+b2−2*a*b*cosα
W Δ ACB:
|AC|2=a2+b2−2*a*b*cosβ⇔
|AC|2=a2+b2+2*a*b*cosα
|BD|2+|AC|2=a2+b2−2*a*b*cosα+a2+b2+2*a*b*cosα⇔
|BD|2+|AC|2=2a2+2b2⇔
|BD|2+|AC|2=2|AB|2+2|BC|2
cnw
======================
α−kąt ostry
β=180−α
cosβ=cos(180−α)=−cosα
W ΔDAB z tw. cosinusów:
|BD|2=a2+b2−2*a*b*cosα
W Δ ACB:
|AC|2=a2+b2−2*a*b*cosβ⇔
|AC|2=a2+b2+2*a*b*cosα
|BD|2+|AC|2=a2+b2−2*a*b*cosα+a2+b2+2*a*b*cosα⇔
|BD|2+|AC|2=2a2+2b2⇔
|BD|2+|AC|2=2|AB|2+2|BC|2
cnw
======================



 jeszcze raz dziękuje
jeszcze raz dziękuje 
