Analiza Nolan: Wyznacz dziedzinę funkcji. Wyznacz maksymalne przedziały monotoniczności funkcji: f(x)= x−3 + (x−3)/(x−4) + (x−3)/(x−4)²+... (szereg geometryczny). Mógłby ktoś rozwiązć?

Qulka: dziedzina |1/(x−4) | <1 wtedy

	(x−3)(x−4)
f(x) =
	x−5

Qulka:

pigor: ..., iloraz q= ¹_x−4 i jeśli |q| <1 ⇔ ¹_{|x−4 |} <1 ⇔ |x−4| >1 ⇔ ⇔ x−4< −1 v x−4>1 ⇔ x< 3 v x > 5 ⇒ szereg f jest zbieżny

	x−3		(x−3)(x−4)
do funkcji f(x)=		⇔ f(x)=		⇔
	1− 1x−4		x−5

	x2−7x+12
⇔ f(x)=		i Df = (−∞;3) U (5;+∞) − szukana dziedzina f. f,
	x−5

teraz licz sobie pochodną f.f i znajdź przedziały domknięte monotoniczności .

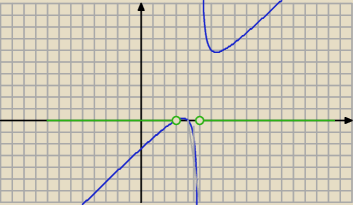
pigor: ... , masz piękny wykres (x=5 ⇔ x−5=0 − równanie asymptoty pionowej) jeszcze znajdź dokładne wartości min/max. funkcji f i masz przedziały jednostronnie domknięte (bo mają być maksymalne) monotoniczności. ...