funkcje trygonometryczne - prosze o pomoc... agatF: Proste dane równaniami y=0,5x+3, y−3=0, x−4=0 ograniczają trójkąt prostokątny. Oblicz tangens większego z kątów ostrych tego trójkąta

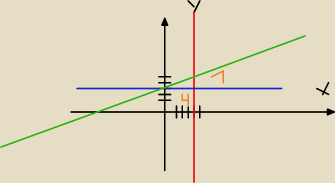
mathalius: Zamieniamy równania: y=1/2x + 3 zielony( Sprawdzamy wartości dla x=4 i x=0) tak aby powstał trojkąt) y=3 niebieski x=4 czerwony Z wykresu mozemy odczytać długości przyprostokątnych 4 i 1. Nie trzeba juz obliczac przeciwprostokatnej, gdyz szukamy tangensa. wczesniej należy się zastanowić który kąt jest większy. wiekszy jest ten który leży przy krótszym boku.

	4
tgα=
	1

agatF: tylko ze mi sie z odpowiedzia nie zgadza... ;\

Nikka:

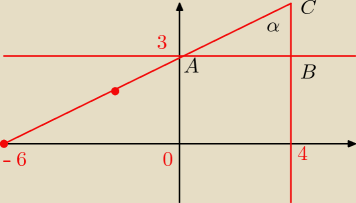
	|AB|
tgα =
	|BC|

A (0,3) B (4,3) C − punkt przecięcia prostych x =4 i y = 0,5x + 3, czyli rozwiązując układ równań otrzymamy C (4,5) Ze wzoru na długość odcinka (gdy znamy współrzędne początku i końca) : |AB| = √(4−0)²+(3−3)² |AB| = 4 |BC| = √(4−4)²+(5−3)² |BC| = 2

	4
tgα =		= 2
	2

Bogdan:

	1
Prosta y =		x + 3 jest nachylona do osi x, a także do prostej y = 3 pod kątem α, którego
	2

	1
tg =
	2

	x		1
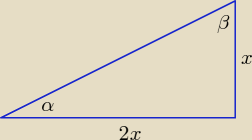
Odczytując z rysunku trójkąta prostokątnego otrzymujemy: tgα =		=		,
	2x		2

	2x
tgβ =		= 2
	x