Zaznaczenie zbiorów na płaszczyźnie (liczby zespolone)
Ania95: Nie mam pojęcia jak się za to zabrać..
Na płaszczyźnie ℂ zaznacz zbiory A∪B jeżeli:
a) A={z: 2≤|z−i|<4}, B={z: |z|<|z−2i|}
3 lis 13:16
PW: Wskazówka:
|z − i| = 4
to zbiór punktów z, których odległość od i jest równa 4 (okrąg o środku i
i promieniu 4).
Zbiór punktów, dla których
|z − i| < 4
to już nie okrąg, ale wnętrze koła.
3 lis 13:40
Janek191:
A − to pierścień bez jednego brzegu ( okręgu )
3 lis 13:46
J:
B − zbiór punktów płaszczyzny,których odległość od punktu (0,0)
jest mniejsza niż od punktu (0,2i) ....czyli pópłaszczyzna pod spodem
symetralnej odcinka (0,2i)
3 lis 14:45
Ania95: czyli jeśli:
b) A={z: |z−2i| < 2}, B={|z+2|≤2} to suma tych zbiorów to połączone dwa wnętrza kół, pierwsze o
środku w punkcie A'(0,2i) i drugie o środku w punkcje B'(−2,0) i też promieniu 2, z tym, że
pierwsze bez krawędzi a drugie z krawędzią −− to jest ok?
f) A={z: Re((1+i)(z+1))<1}, B={z:Im((1+i)(z+1))<1} czyli po wymnożeniu mamy
A={z: Re(1+z + i(z+1))<1}, B={z: Im(1+z + i(z+1))<1}
i co teraz? mam wybrać z A część rzeczywistą, a z B część urojoną? Czy "z" to jest jakaś
liczba rzeczywista czy to liczba zespolona z=a+bi i mam to jeszcze jakoś bardziej rozpisać?
Utknęłam
Nie do końca rozumiem też post J z 14:45, czym jest samo |z| i |z−2i|? Nie wiem jak to sobie
wyobrazić
3 lis 17:24
J:
Iz − z0I = a − zbiór punktów płaszczyzny odległych od z0 o wartość a
IzI = Iz − 0I = a − zbiór punktów płaszczyzny odległych od (0,0) o wartość a
Iz − 2iI = a − zbiór punktów płaszczyzny odległych od (0,2i) o wartość a
3 lis 17:38
Mila:
Od punktu (0,2).
3 lis 17:45
J:
na płaszczyźnie zespolonej moźemy go oznaczyć (0,2i)
3 lis 17:47
PW: W "zwykłej geometrii" na płaszczyźnie zbiór punktów P, dla których
|PA| = |PB|
to symetralna odcinka AB.
W języku liczb zespolonych − pisząc z zamiast P oraz (0,0) = 0 + 0i zamiast A i (0,2) = 0
+ 2i zamiast B mielibyśmy zapis
|z − 0| = |z − 2i|.
Nie ma jednak równości, lecz nierówność
|z − 0| < |z − 2i|.
co oznacza (jak już pisał J), że punktom z jest bliżej do (0,0) niż do (0,2) −
szukane punkty nie leżą na symetralnej odcinka wyznaczonego przez punkty (0,0) i (0,2), ale po
tej stronie symetralnej, po której leży (0, 0).
Warto zrobić rysunek, który pozwoli to lepiej zrozumieć. Gdy już na jednym rysunku umieścisz A
oraz B, to po prostu zakreskować A∪B
3 lis 17:51
Ania95: J: B={z: |z|<|z−2i|} − ale tu nie ma żadnego "=". Jakbym chciała to zaznaczyć to by byl taki "
prostokąt " z jedną ścianą na OX, drugą równoległą do OX, przechodzącą przez 0,i? Dalej nie
rozumiem skąd to się bierze. A wolfram rysuje takie coś
http://m.wolframalpha.com/input/?i=%7Cz%7C<%7Cz-2i%7C&x=0&y=0
I co zrobić dalej z f)?
3 lis 18:00
PW: Nie rozwiązuj zadań maszyną, Ty masz myśleć, a nie "wrzucać do wolframa". Na tym etapie
jest to bardziej szkodliwe niż pomocne.
3 lis 18:15
Ania95: Dlatego pytam czy to jest ok, bo wolfram pokazuje całkiem coś innego, a ja nie mam odpowiedzi
do zadań. Czyli ten prostokąt tak jakby nieskończony na szerokość prostokąt z dwoma bokami
jednymna OX drugim równoległym przechodzącym przez punkt (0,i) jest ok? Czy ktoś mógłby mi
wytłumaczyć skąd to się wzięło i co dalej zrobić z f)?

3 lis 18:27
Mila:
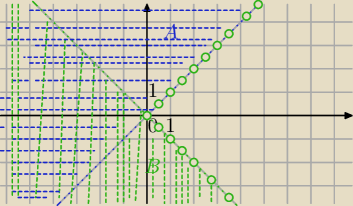
f)
A={z: Re((1+i)(z+1))<1}
Re(z+1+i*z+i)<1, z=x+iy, gdzie x,y∊R
Re(x+iy+1+i*(x+iy)+i))<1
Re([x+1−y]+i*(x+y+1))<1⇔
x+1−y<1⇔x−y<0⇔y>x to jest część płaszczyzny nad prostą y=x
B={z:Im((1+i)(z+1))<1}
Im((1+i)(z+1))<1⇔
x+y+1<1⇔
x+y<0⇔
y<−x to jest część płaszczyzny pod prostą y=−x
A∪B to złączenie zbiorów
3 lis 18:55
Ania95: Bardzo dziękuję Mila

3 lis 19:24
Mila:
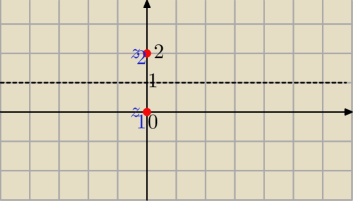
a) zbiór B
B={z: |z|<|z−2i|}
Najlepiej gdybys przemyślała i zrozumiała to, co napisał
PW
albo tak:
z=x+iy gdzie x,y∊R
|x+iy|<|x+iy−2i|
|x+iy|<|x+i*(y−2)|⇔
√x2+y2<
√x2+(y−2)2 /
2
x
2+y
2<x
2+y
2−4y+4⇔
−4y+4>0
−4y>−4
y<1 część płaszczyzny poniżej prostej y=1
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
II sposób
|z−0|=|z−2i| to zbiór punktów leżących na symetralnej odcinka łączącego punkty (0,0) i (0,2).
Ta symetralna to prosta: y=1
Ty masz nierówność :
|z|<|z−2i| musisz wybrać jedną z półpłaszczyzn, teraz wczytaj się w komentarz
PW i
wybierz tę półpłaszczyznę,
jeśli nie wiesz jak, to podam jeszcze inny sposób , jak wybrać, ale to po kolacji.
3 lis 19:39
Ania95: Już rozumiem, że to ta dolna półpłaszczyzna. Pisałam posta w tym samym czasie kiedy PW dodał
swojego i dlatego jego post mi umknął. Dzięki Mila i PW.
3 lis 20:43

 f)
A={z: Re((1+i)(z+1))<1}
Re(z+1+i*z+i)<1, z=x+iy, gdzie x,y∊R
Re(x+iy+1+i*(x+iy)+i))<1
Re([x+1−y]+i*(x+y+1))<1⇔
x+1−y<1⇔x−y<0⇔y>x to jest część płaszczyzny nad prostą y=x
B={z:Im((1+i)(z+1))<1}
Im((1+i)(z+1))<1⇔
x+y+1<1⇔
x+y<0⇔y<−x to jest część płaszczyzny pod prostą y=−x
A∪B to złączenie zbiorów
f)
A={z: Re((1+i)(z+1))<1}
Re(z+1+i*z+i)<1, z=x+iy, gdzie x,y∊R
Re(x+iy+1+i*(x+iy)+i))<1
Re([x+1−y]+i*(x+y+1))<1⇔
x+1−y<1⇔x−y<0⇔y>x to jest część płaszczyzny nad prostą y=x
B={z:Im((1+i)(z+1))<1}
Im((1+i)(z+1))<1⇔
x+y+1<1⇔
x+y<0⇔y<−x to jest część płaszczyzny pod prostą y=−x
A∪B to złączenie zbiorów

 a) zbiór B
B={z: |z|<|z−2i|}
Najlepiej gdybys przemyślała i zrozumiała to, co napisał PW
albo tak:
z=x+iy gdzie x,y∊R
|x+iy|<|x+iy−2i|
|x+iy|<|x+i*(y−2)|⇔
√x2+y2<√x2+(y−2)2 /2
x2+y2<x2+y2−4y+4⇔
−4y+4>0
−4y>−4
y<1 część płaszczyzny poniżej prostej y=1
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
II sposób
|z−0|=|z−2i| to zbiór punktów leżących na symetralnej odcinka łączącego punkty (0,0) i (0,2).
Ta symetralna to prosta: y=1
Ty masz nierówność :
|z|<|z−2i| musisz wybrać jedną z półpłaszczyzn, teraz wczytaj się w komentarz PW i
wybierz tę półpłaszczyznę,
jeśli nie wiesz jak, to podam jeszcze inny sposób , jak wybrać, ale to po kolacji.
a) zbiór B
B={z: |z|<|z−2i|}
Najlepiej gdybys przemyślała i zrozumiała to, co napisał PW
albo tak:
z=x+iy gdzie x,y∊R
|x+iy|<|x+iy−2i|
|x+iy|<|x+i*(y−2)|⇔
√x2+y2<√x2+(y−2)2 /2
x2+y2<x2+y2−4y+4⇔
−4y+4>0
−4y>−4
y<1 część płaszczyzny poniżej prostej y=1
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
II sposób
|z−0|=|z−2i| to zbiór punktów leżących na symetralnej odcinka łączącego punkty (0,0) i (0,2).
Ta symetralna to prosta: y=1
Ty masz nierówność :
|z|<|z−2i| musisz wybrać jedną z półpłaszczyzn, teraz wczytaj się w komentarz PW i
wybierz tę półpłaszczyznę,
jeśli nie wiesz jak, to podam jeszcze inny sposób , jak wybrać, ale to po kolacji.