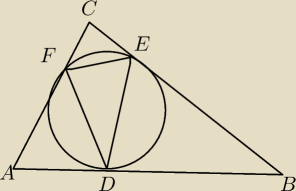
 Punkty D,E,F są punktami styczności okręgu wpisanego w trójkąt ABC z jego bokami. Przyjmujemy,
Punkty D,E,F są punktami styczności okręgu wpisanego w trójkąt ABC z jego bokami. Przyjmujemy,
| α+β | ||
że kąt∡BAC=α, ∡ABC=β oraz ∡FDE=γ. Wykaż, że γ= | . | |
| 2 |
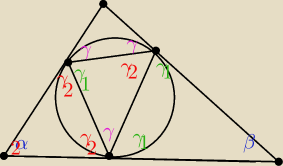 γ+γ1+γ2=180o i α+2γ2=180o i β+2γ1=180o
2γ+2γ1+2γ2=360o
2γ+180o −β+180o −α=360o
2γ −β−α=0
γ+γ1+γ2=180o i α+2γ2=180o i β+2γ1=180o
2γ+2γ1+2γ2=360o
2γ+180o −β+180o −α=360o
2γ −β−α=0
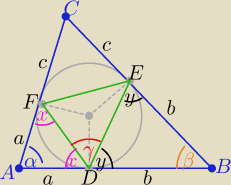 Z twierdzenia o odcinkach stycznych trójkąty
ADF i DBE są równoramienne
2x+α=180o i 2y+β= 180o
Z twierdzenia o odcinkach stycznych trójkąty
ADF i DBE są równoramienne
2x+α=180o i 2y+β= 180o
| α | β | α+β | ||||
to |∡x|= 90o− | i |∡y|= 90o− | to x+y= 180o− | ||||
| 2 | 2 | 2 |
| α+β | ||
|∡γ|= 180o−(x+y)= | ||
| 2 |