arcus kuba: dla jakich argumentów x prawdziwe są tożsamości? cos(2arccosx)=2x²−1

kuba: i drugi przykład arccos[(1−x²)/(1+x²)]=−2arxtgx bardzo dziekuje za pomoc

kuba: a) (2x²−1)∊<−1;1> i x∊<−1;1> b) [(1−x²)/(1+x²)]∊<−1;1>

kuba: nikt nic ?

Mila: 1) Dobrze . warunek: −1≤2x²−1≤1 i x∊<−1, 1> ⇔ x∊<−1, 1> Wtedy: arccosx=α L=cos(2α)=2cos²(α)−1=2*[(cos(arccosx)]²−1=2x²−1=P

kuba: dziekuje @Mila zawsze cos(arccosx)=x i sin(arcsinx)=x

kuba: i jak udowodnic druga tozsamość?

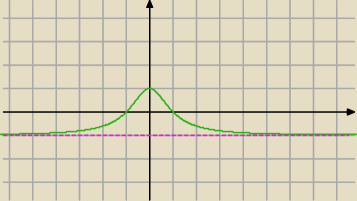
Mila: Dla jakich argumentów x prawdziwe są tożsamości: arccos[(1−x²)/(1+x²)]=−2arctg(x) 1) arctg(x) określony dla x∊R 2) arccos[(1−x²)/(1+x²)] określony dla −1≤[(1−x²)/(1+x²)] ≤1⇔x∊R Dziedziny zgadzają się, teraz zbiory wartości.

	π		π
3) (−		<arctg(x)<		) /*(−2)⇔
	2		2

−π<−2arctg(x)<π 4) arccos[(1−x²)/(1+x²)] ∊<0,π> z (3) i (4) a) 0<−2arctg(x)<π /(−2) czyli arcos[(1−x²)/(1+x²)]≠π⇔ cos(arcos[(1−x²)/(1+x²)])≠cos(π)⇔ [(1−x²)/(1+x²)]≠−1 co zachodzi dla x∊R [ rozwiąż warunek, na wykresie y=(1−x²)/(1+x²)] b) −2arctg(x)>0⇔ arctg(x)<0⇔x<0 Odp. Dla x<0. Nie wiem, czy to wszystko, nie masz odpowiedzi?

Mila: poprawka , bo arccos[..]≥0 to i −2artg(x) ma być ≥0 b) −2arctg(x)≥0⇔ arctg(x)≤0⇔x≤0 odp.x≤0

kuba: niestety odpowiedzi nie mam, ale dziękuję ślicznie

Mila: